环板式针摆行星减速器箱体的模态分析
2013-06-17 by:广州有限元分析、培训中心-1CAE.COM 来源:仿真在线
振动系统的固有特性一般指系统的固有频率和振型,是系统的动态特性之一,它对系统的动态响应,动载荷的产生与传递,及系统振动的形式等有重要影响。模态分析是用来确定结构固有特性的一种技术,是所有动态分析类型最基础的内容。环板式针摆行星减速器是一种高承载能力和高传动效率的新型传动装置,作为整机的主要承力部件,减速器箱体的动态性能影响整个系统的振动特性,因此,对减速器箱体进行模态分析,是研究整个减速器振动特性的基础。
目前,国际较大型的面向工程的有限元通用软件达到几百种,包括:ANSYS,NASTRAN,ASKA,ADINA,I-DEAS等,笔者用ANSYS软件对环板式针摆减速器箱体进行模态分析,求解箱体的固有特性,为研究整个系统的动态特性奠定基础。
1 箱体有限元模型的建立
ANSYS是一个通用、大型的有限元分析软件,在进行ANSYS分析前,必须先建立几何模型。对于ANSYS软件来说,它提供3种模型生成方法,即直接生成、实体建模和模型导入。对箱体这样的复杂结构,采用模型导入的方法。
以文献的图3中的双电机驱动双曲柄四环板式针摆行星减速器箱体为研究对象,在proe中建立箱体模型,通过配置接口软件,将模型直接导人ANSYS。在模型导人ANSYS前,对箱体的固有特性影响很小的一些微小结构进行忽略或简化,如凸台,放油孔,吊孔环等,可提高运算速度,节省计算空间。假设箱体端盖通过螺栓与箱体主体刚性连接,在建模时作为整体考虑。箱体的材料为各向同性材料,需要输入的材料性能参数有:弹性模量EX = 148GPa,泊松比NUXY=0.31,密度ρ=7330kg/mm3。
2 网格划分和约束条件
2.1 网格划分
对箱体进行网格划分时,采用的单元是Solid 92十节点四面体单元,模型最终划分为57659个单元,共有100855个节点。生成的模型如图1所示。
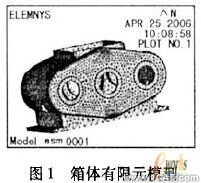
2.2约束条件
由于减速器箱体是通过地角螺栓与地基相连,因此在与地基相接触的底面施加3个位移约束,如图2所示。
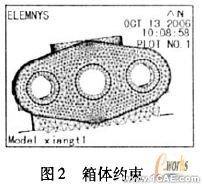
3 ANSYS固有特性的计算方法
由弹性力学有限元法,可得箱体的运动微分方程:
![]()
式中:M,C,K分别为总体质量、阻尼和刚度矩阵;![]() 分别为结构的加速度、速度、位移和激振力向量。
分别为结构的加速度、速度、位移和激振力向量。
若无外力作用,即F(t)=0,则得到系统的自由振动方程。在求结构自由振动的频率和振型,即求结构的固有频率和固有振型时,阻尼对其影响不大,因此阻尼项可略去,这时无阻尼自由振动的运动方程为:
![]()
其对应的特征方程为:
![]()
式中:ω为系统的固有频率.
在ANSYS中,求解模型的固有频率和振型有6种:Subspace法、Block Lenczos法、PowerDynamics法、Reduced法、Unsymmebic法、Damped法。如图3所示。

图3 箱体前六阶振型图
对箱体的分析采用Block Lenczos法。这种方法求解精度高,计算速度较快,适用于大型对称特征值求解间题,是较理想的求解方法。
4 箱体有限元分析结果
对图1中的环板式针摆传动箱体有限元模型进行求解,可求出全部的固有频率和振型。但因低阶模态对振动系统影响较大,故常取前10阶即可。环板示赚十摆传动箱体的固有频率如表1所示。
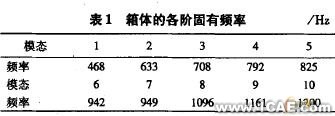
因篇幅有限,仅列出环板式针摆行星传动箱体的前六阶振型图如图3所示。
5 结论
(1)建立环板式针摆传动箱体的有限元模型,并对该模型进行有限元模态分析,求出环板式针摆行星传动箱体的固有频率和振型。
(2)利用振型图和动画显示.可直观地分析环板式针摆行星传动箱体的动态特性,为以后整个系统的动态响应分析和计算奠定基础。
相关标签搜索:环板式针摆行星减速器箱体的模态分析 Fluent、CFX流体分析 HFSS电磁分析 Ansys培训 Abaqus培训 Autoform培训 有限元培训 Solidworks培训 UG模具培训 PROE培训 运动仿真






