CAE在采样头设计中的应用
2013-06-07 by:广州有限元分析、培训中心-1CAE.COM 来源:仿真在线
本文针对某种型号的悬臂式采样头在设计过程中涉及的抵抗变形的能力及其破冰能力,对其进行不同工况下的有限元分析。在进行应力分析的基础上,利用第三强度理论,对结构的强度进行校核,进而指导了设计的改进。
作者: 姜峰 贺成柱 来源: e-works
关键字: CAE ansys 悬臂式采样头 强度理论 变形 破冰
1 引言
20世纪70年代以来,我国煤质分析制样和分析化验的仪器设备已经发展到相当规模,不仅种类齐全,而且正逐步实现自动化,有的已经达到国际水平。但在机械化采样和机械化制样联合系统方面仍发展缓慢。悬臂式采制样设备是为解决上述问题由我院自行研制的一套适用于电厂、煤矿的机械化采制样系统。
2 结构的有限元模型的建立
结构的主体是采样头的悬臂,可以看作是梁结构,本文从计算结果的精确性和仿真的方便,对该部分采用ANSYS软件自带的BEAM3单元,该单元是具有拉伸、压缩和弯曲功能的单轴单元,具有X和Y方向两个平移自由度和绕Z轴的一个转动自由度,并具有计算应力刚化,大变形和单元生死的功能。
在整体建模中,单元的合理连接与节点自由度的合理匹配与否,将直接影响模型的受力和传力特征。在结构中单元和单元之间的连接采用ANSYS提供的节点耦合方式,强制两个节点的平动自由度一致,而释放转动自由度,从而实现铰接关系。
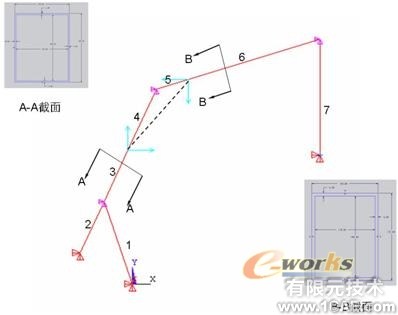
图1 悬臂机构简化图
对于文中采用的BEAM3单元,需要输入的实常数有截面的面积,截面的惯性矩和等效高度。由于BEAM3单元不具备截面定义的功能,对于本结构设计时定义的特殊的截面形状,通过材料力学的知识计算该截面的惯性矩进行等效。
对于结构的边界条件的处理。液压油缸与一节臂之间,一节臂与二节臂之间,二节臂与采样头之间采用接点耦合的方式强制两个平动自由度一致,而释放销轴的转动自由度,实现铰接关系。一节臂的下端与液压油缸的下端采用铰支约束。采样头的末端采用固支约束。为了计算采样头的破冰能力,将结构上部的液压油缸(图1中虚线所示)拆除,将其作用力等效到结构上,等效的作用力大小为(1)
其中(2)
本文的强度校核就采用上式的方式进行检验。本结构采样头的悬臂采用16Mn钢材料,其屈服极限为σs=345MPa。
4 结构整体的分析结果
4.1 远点采样时分析结果。
表1 结构各单元的最大应力(单位:MPa)
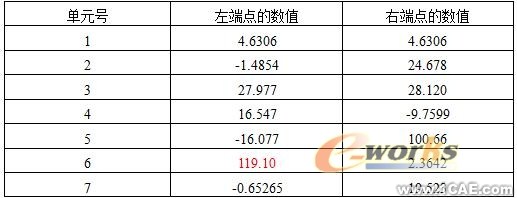
表2 结构各单元的最小应力(单位:MPa)
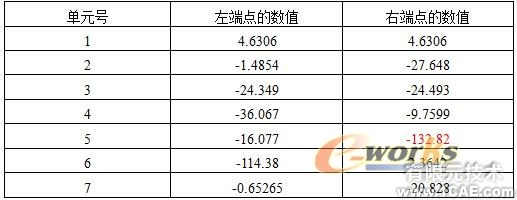
4.2 近点采样时分析结果 相关标签搜索:CAE在采样头设计中的应用 Fluent、CFX流体分析 HFSS电磁分析 Ansys培训 Abaqus培训 Autoform培训 有限元培训 Solidworks培训 UG模具培训 PROE培训 运动仿真
此时
表3 结构各单元的最大应力(单位:MPa)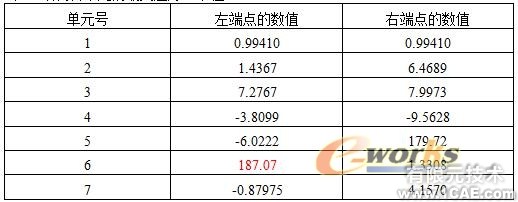
表4 结构各单元的最小应力(单位:MPa)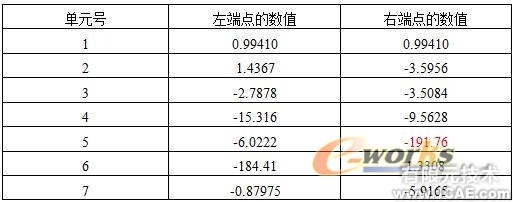
此时
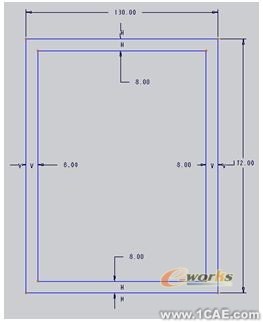
图2 截面B-B增强后的截面形状
表5 改进后近点采样结构各单元的最大应力(单位:MPa)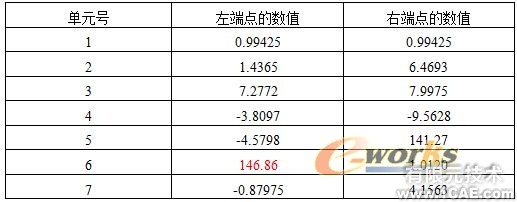
表6 改进后近点采样结构各单元的最小应力(单位:MPa)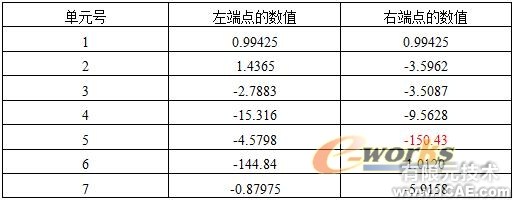
此时
对于采样头的破冰能力如表7所示,ANSYS计算的数据显示远点采样时折合为1121.9kg,近点采样时折合为1512.3kg,二者的破冰能力均在1吨以上。
对于结构在进行远点采样时的整体抵抗变形的能力也很强,计算的结构在极限受力状态下的变形对于整个结构来说完全可以忽略不计。
5 结论与建议
对截面B-B进行截面的改进,使采样头均能满足远点采样和近点采样时的强度要求;在分析中可以发现,采样头的破冰能力和在进行采样时的整体抵抗变形的能力是比较强的。






