搜索铁道客车变形碰撞有限元分析
2013-06-23 by:广州有限元分析、培训中心-1CAE.COM 来源:仿真在线
关键字:CAE 有限元 碰撞 变形 仿真
利用PAM-CRASH对25型铁道客车进行了大变形碰撞仿真研究。 通过设置不同部分壳体单元的不同厚度,巧妙地处理了车体钢骨架与车体侧墙板及其它各种板件的焊接关系。根据仿真计算结果分析了车身主要吸能部件的变形规律,找出了设计中的一些不足之处,并提出了一些相应的改进措施。假人模型中的有关头部伤害指标和大腿伤害指标的计算结果表明,列车碰撞及其碰撞后乘客与乘客,或乘客与车内物体的二次碰撞是导致乘客伤害的关键原因。利用PAM-CRASH的并行功能,进行了六百万自由度的25型铁道客车之间的碰撞分析。
1 引言
在汽车工业领域中,大变形碰撞是一项倍受重视的被动安全研究,他们不但用实车实物在专用的实验车间里不惜代价地进行破坏性实验,同时,还广泛采用计算机数值仿真手段对结构破坏过程进行高速碰撞模拟,从而对设计的安全性进行分析和评价[1]。在汽车安全领域,国内外都制订了专门的被动安全法规,并开发了一些安全保护设施,例如安全带,气囊等。
同其它交通工具相比,列车在方便,准时和运输效率方面非常有优势。同汽车碰撞事故相比,虽然列车发生碰撞的概率要小于汽车发生碰撞的概率,然而一旦发生意外事故,则会带来严重的人和财务损失。例如1998年6月4日在德国的 Eschede 发生的由于脱轨造成的列车事故,它造成了98人死亡,200多人受伤的严重后果。鉴于此,许多国家为了使事故造成的损失最小化在设计车辆时都充分考虑车辆的耐撞性。从1999年起,美国开始要求在高速列车 TIER II (商业速度为 200—240 kph )上必须有列车防撞性设计与评估。在不久的将来,欧洲也会把列车防撞性纳入 UIC 的规则中。
研究车辆大变形碰撞的方法有理论研究,实物实验和数值仿真三种。虽然理论研究和实物实验不可缺少,但是车辆大变形碰撞研究的本身性质决定,数值仿真应成为主要的研究方法。随着计算机的发展和显式仿真软件,如PAM-CRASH 的成熟,成功的工业案例表明,仿真方法完全能胜任大部分车辆大变形碰撞的研究。利用仿真方法,Alstom 公司1996 年进行了高速列车 TGV的开发研究;Siemens 公司1999年进行了高速列车的缓冲器研究;韩国铁道科学研究院对 KHST进行了耐撞性优化设计研究[2]。中国从1999年开始对列车零部件及其一些简单的车辆模型进行了大变形碰撞仿真研究[3][4]。
利用PAM-CRASH对25型铁道客车进行了大变形碰撞仿真研究。基于实际的 25B 车体 CAD 图形,建立了全壳体单元的有限元模型,单车模型的规模将近25万节点。研究了车体碰撞的多种的工况,如车与固定的刚性墙,车与变形体,单车体与单车体,两节车体与两节车体的正面碰撞以及车体与刚性墙斜撞后的脱轨现象。在单车与刚性墙的正撞模型中,随机地放置了一些假人模型,研究了在列车碰撞后,假人与座椅,假人与假人的二次碰撞响应。
2 大变形碰撞虚功方程及其离散形式
文献[5]严格地证明了将接触看成未知面力的虚功方程可写成如下的形式
其中Γf表示应力边界,ΓC表示可能接触边界,ρ表示密度,δU表示虚位移,σ表示柯西应力张量,对于弹塑性问题,应力应变的增量关系式为[6]
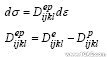
其中弹性矩阵和塑性矩阵的一般形式是
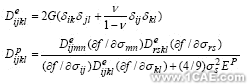
式中材料塑性模量可由应力对等效塑性应变变分得到
;现时屈服应力σs和f与后继屈服函数相关。本文采用Von Mises屈服准则,各向同性硬化的后继屈服函数可以表示为
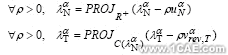
由[7]可知,对于每个接触对α,在局部坐标系下,定义
为法向相对位移,
为法向和切向作用力,
为切向相对速度,刻画接触关系的Signorini条件和Coulomb干摩擦条件可表示为
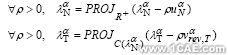
PROJ 表示正交投影,
。以R表示整体坐标系下的作用力,它可由局部坐标系下的作用力
表示,类似[7],可推导得到虚功方程(1)的全离散形式如下
其中h是时间步长,I表示时间步,F 表示内力,体力和面力之和,R为离散的摩擦力。在显式算法中当采用减缩积分时,为了处理由于减缩积分而引起的沙漏问题,需要引入阻尼力,即公式(6)中的F 表示内力,体力,面力以及沙漏阻尼力之和。
3 车辆碰撞的有限元模型
25型客车车体钢结构为全钢焊接结构,由底架、侧墙、车顶和端墙四部分焊接而成。在侧墙、端墙、车顶钢骨架外面,在底架钢骨架的上面分别焊有侧墙板、端墙板、车顶板和纵向波纹地板及平地板,形成一个上部带圆弧,下部为矩形的封闭壳体,俗称薄壁筒形车体结构。壳体内面或外面用纵向梁和横向梁、柱加强,形成整体承载的合理结构。本文利用壳体单元对薄壁筒形车体结构进行网格剖分,包括座椅和hybrid III假人的三维有限元模型如图1所示,其中转向架为刚性壳体单元,虚线表示钢轨。
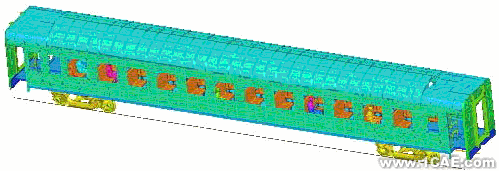
图1:三维有限元模型
图1中的车内hybrid III假人的放置是随机的,如图2所示
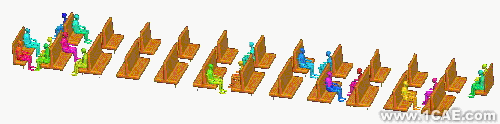
图2 座椅和假人
底架、侧墙、车顶和端墙四部分之间焊接关系是线焊关系,因此可以假定焊接处在大变形碰撞过程中总保持连续。底架、侧墙、车顶和端墙被钢骨架分成不同的小部分,底架、侧墙、车顶和端墙与钢骨架焊接处壳体单元的厚度为两结构的厚度的和,其它小部分壳体单元的厚度为各自本身的厚度。接触关系包括车体与障碍物接触,车轮与轨道接触,车轮与地面接触,车体自接触,假人与座椅以及假人与假人的接触。除车体与障碍物接触给定摩擦系数外,其它的接触关系只考虑法向接触。
4 数值实验及其分析
汽车碰撞的实物研究和仿真研究开展了很多年,特别在国外的汽车科技发达的国家,其安全法规及其安全措施已比较成熟。与汽车碰撞研究相比,虽然国内外开展了一定的研究,但是需要进行的工作还很多。
本文利用PAM-CRASH对25型铁道客车进行了大变形碰撞仿真研究。基于实际的 25B 车体 CAD 图形,建立了全壳体单元的有限元模型,单车模型的规模将近25万节点。研究了车体碰撞的多种的工况,如车与固定的刚性墙,车与变形体,单车体与单车体,两节车体与两节车体的正面碰撞以及车体与刚性墙斜撞后的脱轨现象。在单车与刚性墙的正撞模型中,随机地放置了一些假人模型,研究了在列车碰撞后,假人与座椅,假人与假人的二次碰撞响应。
4.1车体与刚性墙的正面碰撞
文[8]给出了设计耐撞击的客运列车的一些基本性的原则,即要求车体结构按前、中、后三种纵向刚度设置,前后两部分为可以产生塑性变形的弱刚度吸能结构,中间部分为仅产生弹性变形的强刚度弹变结构。本文进行了初速度为15m/s (54Km/h)车体与固定刚性壁的正面碰撞分析,最后的变形结果如图3所示,车体头部在0ms, 80ms 200ms时刻的变形图分别如图4的a,b,c所示。
图3 车体最后的变形
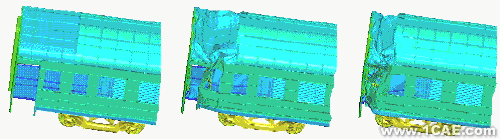
a 0ms b 80ms c 200ms
图4 车体头部在不同时刻的变形
由图3和图4可看出,车体的头部发生了很大的塑性的变形,车体的中部和尾部基本上没发生塑性变形。当列车发生正面碰撞事故时,非端部编组的车辆的头部和尾部都将同其它的车辆或机车发生碰撞,因而车辆的前部和尾部都将发生变形。由于车体的前后是对称结构,由图3和图4的变形结果可分析出,车体前后两部分的刚度比中部的刚度要弱。
初速度为15m/s (54Km/h)车体与固定刚性壁的正面碰撞和初速度为30m/s(108km/h)车体与固定刚性壁的正面碰撞过程的能量变化曲线分别如图5的a,b所示。由图5可知,系统的动能在碰撞过程中,基本上被车体的塑性变形所吸收。牵引梁是主要吸能部件,但其吸能性随吸能总吸收的能量的增加而降低。
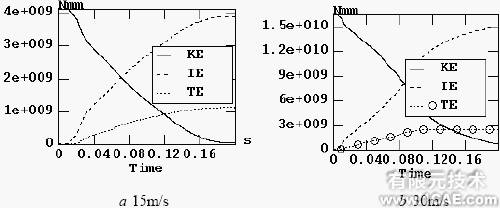
图5 能量变化曲线,KE,IE,TE 分别表示动能,内能,牵引梁吸收的能量
当车体的初速度为15m/s (54Km/h)时,其吸收的能量接近总的能量的1/3,但是当车体的初速度为30m/s(108km/h)时,其吸收的能量却不到总的能量的1/5。初速度为15m/s (54Km/h)车体与固定刚性壁的正面碰撞过程中其底架的牵缓端枕梁结构的变形如图6所示。如图6所示,牵引梁吸能性下降的原因是在碰撞过程中牵引梁在其与端梁相交处发生了弯曲失效。理论分析表明,当一个梁沿纵向承受大变形碰撞后,如果发生弯曲而不是沿纵向压塌,那么,该梁就不是一个好的吸能结构。该车的这种结构显然不能很好地吸收车受撞后的动能。我们知道,结构吸能特性不仅取决于其材料性质,也与其几何形状与尺寸有关,从碰撞安全保护角度出发,建议改进牵引梁的结构,即增大其与断梁相交部分的刚度。
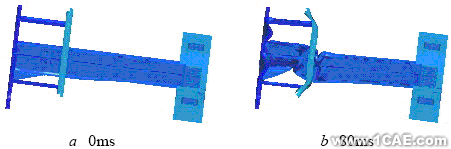
图6 牵缓端枕梁结构的变形
4.2 乘员二次碰撞响应
列车撞击事故中,驾驶员的伤害很大程度上来自于机车与其它物体的碰撞;客车车厢内的乘客的伤害既与列车碰撞有关,也与列车碰撞后乘员的二次碰撞有关,即乘员与乘员,或乘员与车内其它较刚性物体的碰撞。为了研究乘员的二次碰撞响应,如图2所示,本文在车内随机地放置了一些假人,假人的编号按从前到后从左到右的顺序方式进行。车体以15m/s (54Km/h)的初速度与固定刚性壁发生正面碰撞,撞击过程中前四个假人在初始时刻和最后时刻的运动和变形如图7所示,前四个假人的头部伤害指标HIC如表1所示,第三个和第四个假人大腿轴向力随时间的变化分别如图8的a,b所示。
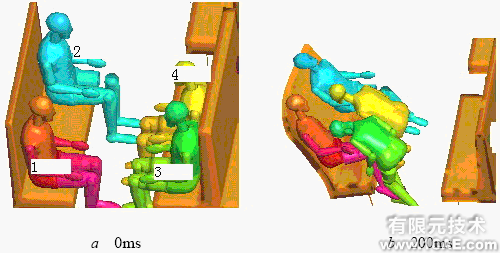
图7 前四个假人的运动和变形
表1 前四个假人头部伤害指标
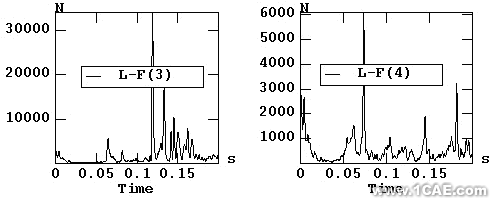
a 第三个假人 b 第四个假人
图8 大腿轴向力与时间的关系
由表1和图8的 a 可知,第三个假人的头部伤害指标HIC 1255 超过了允许的伤害指标 1000,而且其大腿的轴向力30kn也大于标准的10kn,仿真数据表明,撞击过程中第三个假人将会非常危险。其它的假人危险性不是很大,如第四个假人的大腿轴向力在标准范围内,第一,第二和第四个假人的头部损伤指标也没有超标。相对来说,第一个假人的头部损伤指标比第二和第四个假人的头部损伤指标要大。表1和图8的数据与图7中四个假人的运动与变形情况是吻合的,由图7可知,第三个不但由于列车的碰撞而突然向前运动,而且与第一个假人发生了二次碰撞。上述数据说明,客车车厢内的乘员的伤害,不但与列车的碰撞有关,而且与乘员的二次碰撞有非常大的关系。为了减少乘员在撞击事故中的伤害,除了优化车体的设计提高其耐撞性,应采取措施尽量避免乘员的二次碰撞。如将车厢内的茶几或其它非常刚性的物体的表面套上一些较软的物体;将行李假设计成封闭的行李厢,以免行李在列车撞击时飞出来与乘员发生二次碰撞;在座椅上设计安全带等等。
4.3 并行处理
列车碰撞仿真研究与汽车碰撞仿真研究相比,其最大的难点就是其规模大,而且碰撞作用的时间长。虽然同样的程序既能做汽车碰撞仿真研究,也能完成列车碰撞仿真研究,但列车碰撞仿真研究的计算时间有时让人难以忍受。解决这一难题的最好办法就是利用并行技术来大大的缩短计算时间。对于单元数目为 268119 的25型铁道客车车辆模型,不同数目 CPU 的计算时间对比如表2所示。
表2 计算机运行时间对比
最初的并行软件只是单元计算和求解器并行化,现在的并行软件发展到了基于区域分解的并行处理,例如并行的 PAM-CRASH 软件。前处理中用户根据 CPU的数目将需要计算的区域划分成一些相对来说比较均匀的子区域,程序能自动地使用不同的 CPU 来计算不同字区域的各种场。对于每个子区域来说,需要求解的如下方程与方程(6)比较类似,
其中下标i表示子区域,λij 表示处理子区域i和子区域j公共边界的连续性而引入的内部界面力,与接触力一样,它也是未知的,在迭代过程中由子区域边界的连续性得到,ui(I+1)-uj(I+1_=0
本文利用并行技术和广州超级计算中心的并行环境进行了两节车与两节车的对撞分析。模型中总的节点数为 1004434,壳单元数为988528,刚体单元为 7046,利用32 CPU 花费 7.3就完成了碰撞分析,碰撞后的变形图如图9所示。
图9 两节车体与两节车体碰撞的变形情况
5 结论和讨论
利用PAM-CRASH对25型铁道客车进行了大变形碰撞仿真研究。基于实际的 25B 车体 CAD 图形,建立了全壳体单元的有限元模型。研究了车体碰撞的多种的工况,如车与固定的刚性墙,车与变形体,单车体与单车体,两节车体与两节车体的正面碰撞。在单车与刚性墙的正撞模型中,随机地放置了一些假人模型,研究了在列车碰撞后,假人与座椅,假人与假人的二次碰撞响应。数值结果表明,该车总体满足设计规则,即车体前后部分刚度较弱车体中间的刚度较大。牵引缓冲梁是主要的吸能结构,在变形过程中出现了弯曲失效,可以通过加强其失效部位的刚度来提高其吸能性。
参考文献
1 钟志华,汽车耐撞性分析的有限元法 [J],汽车工程,1994,16(1):1-6。
2 Jeong-seo Koo, Tae-Soo Kwon, Hyun-Jik Cho, 韩国高速铁路防撞设计与评估 [J],将发表于中国铁道科学学报,2004(1)。
3 谢素明,兆文忠,闫雪冬,高速车辆大变形碰撞仿真基本原理及应用研究 [J] ,铁道车辆,2001(8), P1-4。
4 姚松,田红旗,车辆吸能部件的薄壁结构碰撞研究 [J],中国铁道科学,2001(22);2:55-60。
5 Laursen TA,Simo JC. A continuum-based finite element formulation for the implicit solution of multi-body, large deformation frictional contact problems[J], Int. J. Num. Meth. Engeg 1993;36:3451-85。
6 王勖成,邵敏,有限单元法基本原理和数值方法[M],清华大学出版社,1997。
7 Frank Jourdan,Pierre Alart,Michel Jean,A Gauss-Seidel like algorithm to solve frictional contact problems[J] , Comput. Methods Appl. Meth. Engrg 155(1998) 31-47。
相关标签搜索：铁道客车变形碰撞有限元分析 Fluent、CFX流体分析 HFSS电磁分析 Ansys培训 Abaqus培训 Autoform培训 有限元培训 Solidworks培训 UG模具培训 PROE培训 运动仿真
