有限元分析中的单位问题

2013-06-22  by:广州有限元分析、培训中心-1CAE.COM  来源:仿真在线

大多数有限元计算程序都不规定所使用的物理量的单位,不同问题可以使用不同的单位,只要在一个问题中各物理量的单位统一就可以。但是,由于在实际工程问题中可能用到多种不同单位的物理量,如果只是按照习惯采用常用的单位,表面上看单位是统一的,实际上单位却不统一,从而导致错误的计算结果。

    比如,在结构分析中分别用如下单位:长度 – m;时间 – s;质量 – kg;力 - N;压力、应力、弹性模量等 – Pa,此时单位是统一的。但是如果将压力单位改为 MPa,保持其余单位不变,单位就是不统一的;或者同时将长度单位改为 mm,压力单位改为 MPa,保持其余单位不变,单位也是不统一的。由此可见,对于实际工程问题,我们不能按照手工计算时的习惯来选择各物理量的单位,而是必须遵循一定的原则。

    物理量的单位与所采用的单位制有关。所有物理量可分为基本物理量和导出物理量,在结构和热计算中的基本物理量有:质量、长度、时间和温度。导出物理量的种类很多,如面积、体积、速度、加速度、弹性模量、压力、应力、导热率、比热、热交换系数、能量、热量、功等等,都与基本物理量之间有确定的关系。基本物理量的单位确定了所用的单位制,然后可根据相应的公式得到各导出物理量的单位。具体做法是:首先确定各物理量的量纲,再根据基本物理量单位制的不同得到各物理量的具体单位。

    基本物理量及其量纲:

· 质量 m;
· 长度 L;
· 时间 t;
· 温度 T。

    导出物理量及其量纲:

· 速度:v = L/t;

· 加速度: a = L/t2;

· 面积: A = L2;

· 体积: V = L3;

· 密度:ρ= m/L3;

· 力: f = m·a = m·L/t2;

· 力矩、能量、热量、焓等: e = f·L = m·L2/t2;

· 压力、应力、弹性模量等: p = f/A = m/(t2·L) ;

· 热流量、功率:ψ= e/t = m·L2/t3;

· 导热率: k =ψ/ (L·T) = m·L/(t3·T);

· 比热: c = e/(m·T) = L2/(t2·T);

· 热交换系数: Cv = e/(L2·T·t) = m/(t3·T)

· 粘性系数: Kv = p·t = m/(t·L) ;

· 熵: S = e/T = m·l2/(t2·T);

· 质量熵、比熵: s = S/m = l2/(t2·T);

    在选定基本物理量的单位后,可导出其余物理量的单位,可以选用的单位制很多,下面举两个常用的例子。

    1 基本物理量采用如下单位制:

· 质量 m – kg; (应该采用Mg单位才统一,具体可以参考MSC.MARC中的材料库统一单位,推导)
· 长度 L – mm;
· 时间 – S;
· 温度 – K (温度 K与 C 等价)。

    各导出物理量的单位可推导如下,同时还列出了与 kg-m-S 单位制或一些常用单位的关系:

· 速度: v = L/t = mm/S = 10-3 m/S;

· 加速度: a = L/t2 = mm/S2 = 10-3 m/S2;

· 面积:A = L2 = mm2 = 10-6 m2;

· 体积:V = L3 = mm3 = 10-9 m3;

· 密度:ρ= m/L3 = kg/mm3 = 10-9 kg/m3 = 10-6 g/cm3;

· 力: f = m·L/t2 = kg·mm/S2 = 10-3 kg·m/S2 = mN (牛);

· 力矩、能量、热量、焓等:e = m·L2/t2 = kg·mm2/S2 = 10-6 kg·m2/S2 = µ J (焦耳);

· 压力、应力、弹性模量等:p = m/(t2·L) = kg/(S2·mm) = 103 kg/(S2·m) = kPa (帕);

· 热流量、功率:ψ= m·L2/t3 = kg·mm2/S3 = 10-6 kg·m2/S3 = µ w (瓦);

· 导热率:k = m·L/(t3·T) = kg·mm/(S3·K) = 10-3 kg·m/(S3·K);

· 比热:c = L2/(t2·T) = mm2/(S2·K) = 10-6 m2/(S2·K);

· 热交换系数:Cv = m/(t3·T) = kg/(S3·K);

· 粘性系数:Kv = m/(t·L) = kg/(S·mm) = 103 kg/(S·mm);

· 熵:S = m·L2/(t2·T) = kg·mm2/(S2·K ) = 10-6 kg·m2/(S2·K );

· 质量熵、比熵:s= L2/(t2·T) = mm2/(S2·K ) = 10-6 m2/(S2·K );

    基本物理量采用如下单位制:

· 质量 m – g;

· 长度 L – µm (10 6 m);

· 时间 – mS (10–3 S);

· 温度 – K (K与 C 等价)。

    各导出物理量的单位可推导如下,同时还列出了与 kg-m-S 单位制或一些常用单位的关系:

· 速度:v = L/t = µm/mS = 10-3 m/S;

· 加速度:a = L/t2 = µm/mS2 = m/S2;

· 面积:A = L2 = µm2 = 10-12 m2;

· 体积:V = L3 = µm3 = 10-18 m3;

· 密度:ρ= m/L3 = g/µm3 = 10-21 kg/m3 = 10-12 g/cm3;

· 力: f = m·L/t2 = g·µm/mS2 = 10–3 kg·m/S2 = mN (牛);

· 力矩、能量、热量、焓等:e = m·L2/t2 = g·µm2/mS2 = 10 -9 kg·m2/S2 = 10-9 J (焦耳);

· 压力、应力、弹性模量等: p = m/(t2·L) = g/(mS2·µm) = 109kg/(S2·m) = 109Pa (帕) = GPa;

· 热流量、功率:ψ= m·L2/t3 = g·µm2/mS3 = 10-6 kg·m2/S3 = 10-6 w (瓦);

· 导热率:k = m·L/(t3·T) = g·µm/(mS3·K) = kg·m/(S3·K);

· 比热:c = L2/(t2·T) = µm2/(mS2·K) = 10-6 m2/(S2·K);

· 热交换系数: Cv = m/(t3·T) = g/(mS3·K) = 103 kg/(S3·K);

· 粘性系数: Kv = m/(t·L) = g/(mS·µm) = 106kg/(S·mm);

· 熵: S = m·L2/(t2·T) = g·µm2/(mS2·K ) = 10-9 kg·m2/(S2·K );

· 质量熵、比熵: s = L2/(t2·T) = µm2/(mS2·K ) = 10-6 m2/(S2·K );

由此可见,掌握了单位之间变换的方法,就可以根据自己的需要来选择合适的单位制。更多的例子见表1。表2给出了几种单位制与 kg-m-S 单位制之间的换算因子

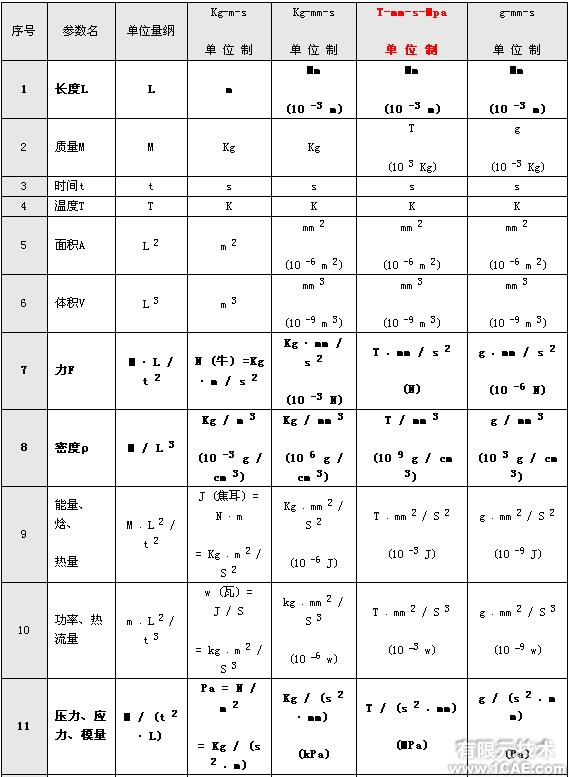
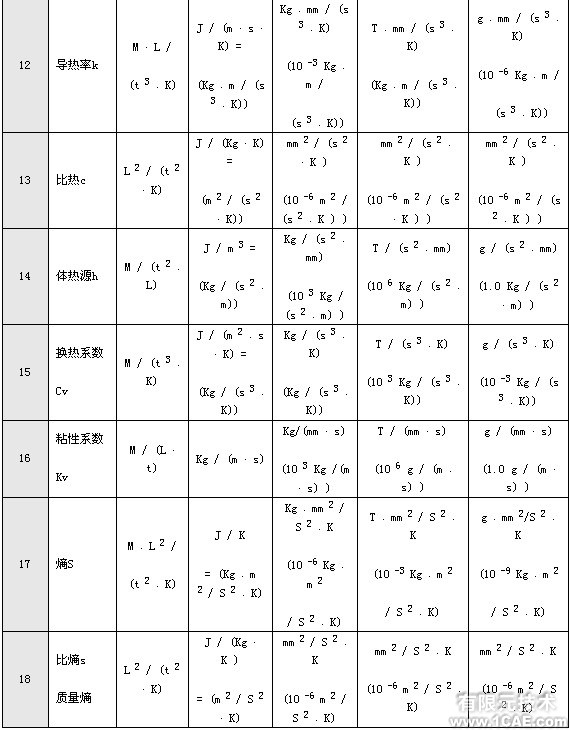
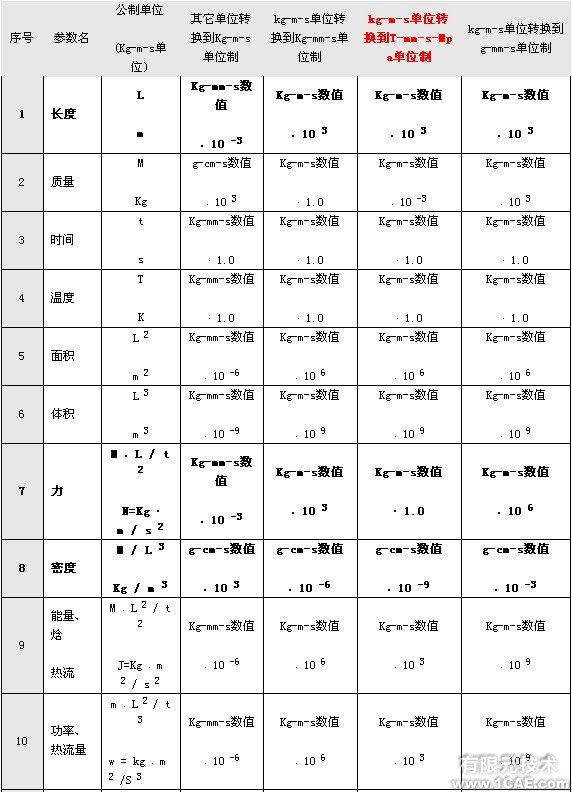
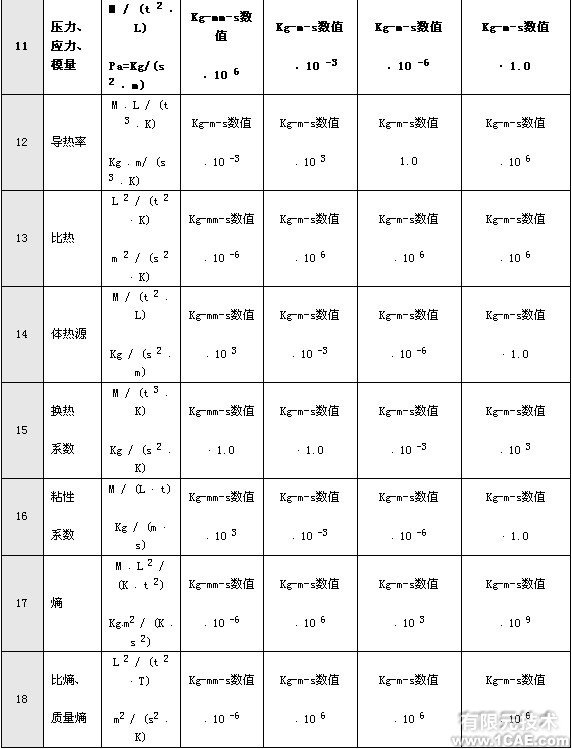
    注:后三列中给出的是将kg-m-S 单位制中的数值转换到其它单位制时 (在准备输入数据时) 所乘的因子;如果需要将其它单位制中的数值转换到kg-m-S 单位制 (在分析计算结果时),则应该除以该因子。

相关标签搜索：有限元分析中的单位问题 Fluent、CFX流体分析 HFSS电磁分析 Ansys培训 Abaqus培训 Autoform培训 有限元培训 Solidworks培训 UG模具培训 PROE培训 运动仿真