搜索声悬浮的实验研究及模拟分析
2013-06-18 by:广州有限元分析、培训中心-1CAE.COM 来源:仿真在线
声悬浮是一种新型无容器处理技术,它实现了材料与容器壁的无接触状态,从根本上避免了由容器壁引起的污染和异质形核,对研究液体的物理性质、过冷和凝固过程具有重要的科学意义。与其他悬浮技术相比,声悬浮主要有两个优点:一是对处理材料没有电磁学性质上的要求,二是悬浮与加热分开进行,可以避免过热产生的滴流现象,特别适用于低熔点合金及一些无机物的无容器处理,同时还为外层空间环境中高性能材料的制备创造了条件。
获得较大的悬浮力和较高的悬浮稳定性是声悬浮研究中的两个关键问题。声悬浮技术借助超声波产生的声辐射力来平衡物体的重力,从而实现物体的悬浮。声悬浮过程中悬浮区域的入射声场分布情况对悬浮性能有着重要的影响,而对于形状复杂的谐振腔,很难用解析的方法得到声场的分布情况。针对这种情兄,本文结合声悬浮的基本原理及实验过程中的一些规律,采用有限元方法对两种不同形状的谐振腔所产生的声场进行了计算和模拟,以此分析声悬浮装置的几何结构对悬浮性能的影响。
1 实验条件及实验研究
图1是自行研制的单轴式声悬浮装置的结构简图,它由H66MC型超声波发生器、压电式功率超声换能器、变幅杆、发射端、反射端、石英管谐振腔及调谐机构组成。超声波发声器输出的频率范围18~20kHz,功率为。0—300W。由超声波发生器激发的超声频振荡经换能器转化为机械振动,再经阶梯式变幅杆将振幅放大。为了使声彼能够较好地向空气中传播,必须使发射端的直径满足d≥λ0,λ0为空气中声波波长,但是为了提高变幅杆的放大倍数,需要使变幅杆输出端直径相对小一些。为了解决这一矛盾,可在变幅杆的输出端连接一个硬铝制成的圆锥形发射盘,这样可以在不减小变幅杆放大倍数的条件下,使声波较好地向空气中辐射。声波在反射端与发射端之间经多次反射迭加后形成驻波,同时产生水平方向上的回复力,使样品能够稳定悬浮于声压波节处。
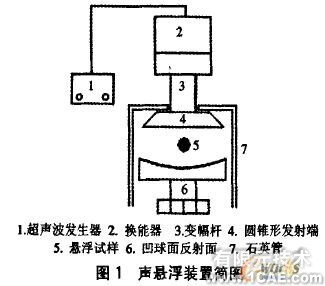
实验时,通过调节反射端与发射端的距离及超声波发生器的功率,使声场处于谐振状态。当谐振区域介质达到谐振时,声场强度达到相应的峰值,这时在悬浮区域会出现一个或几个悬浮力势阱,一个悬浮力势阱对应一个稳定悬浮位置。按照谐振距离从大到小的顺序依次称这些谐振状态为模式1、模式2和模式3等。图2是采用凹球面反射面时,直径为3mm的钢球的声悬浮实验图片。
实验中发现采用不同形状的反射面时,在同一模式下悬浮同一样品,所需的最小电功率不同,所需的最小电功率越小,说明悬浮器的悬浮能力越强。图3给出了分别采用平面反射面和凹球面反射面在不同模式下悬浮直径为2. 5mm的陶瓷球所需的最小电功率。
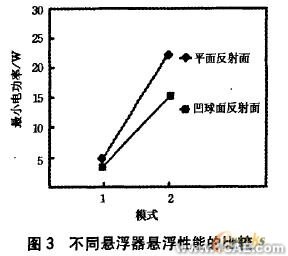
从图中可以看出,采用凹球面反射面的悬浮能力强于平面反射面的悬浮能力。反射面形状为平面(a型谐振腔)时,稳定悬浮时间一般不超过l0min,而反射面形状为凹球面(b型谐振腔)时小球稳定悬浮的时间可达0.5h以上.这说明声悬浮装置的几何结构对悬浮性能有着重要的影响。下面通过数值模拟的方法分析a,b型谐振腔中的声场分布,以此来寻求提高声悬浮性能的途径。
2 计算模型及分析
Bamiatz等基于Gor'kov的理论提出了用以评估各种声场中所悬浮的球形样品的悬浮力和悬浮稳定性的方法,给出理想流体中作用在刚性小球上的声辐射力的时间平均势:
其中:凡是样品的半径(Rs≤λ) , ρf是介质的密度,c是声速,s4和s5分别是样品所在位置的入射声压和流体质点速度的均方值。可根据关系式:
由入射波的速度势中求出,由于样品半径远小于空气中声波波长,所以人射波可以理解为未加人样品时的声场。
发射端的形状主要影响声能的传递效率,对声场的影响不大,因此可将圆锥形发射端等效为圆柱形,采用文献的双圆柱理论模型。两种谐振腔的计算模型类似,不同之处在于反射端形状不同。为了简便,只给出b型谐振腔的计算模型,如图4所示。
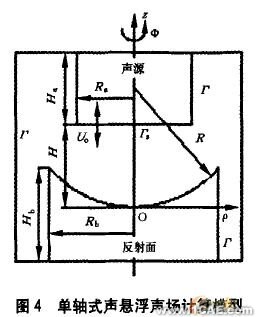
模型上下端分别是声源和刚性反射面,声源以角频率。和速度振幅V0作等幅活塞式简谐振动,周围是刚性谐振腔壁,其法向振速均为零.反射面的表面是球心在圆柱对称轴上的凹球面。在这里采用柱坐标系,z轴为系统的对称轴,原点取在反射面与x轴相交处,T表示所有结构的外表面,T表示声源的下表面。由于系统具有轴对称性,因此,速度势中与环向坐标尹无关,应具有如下形式:
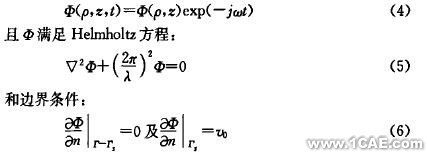
对整个区域Ω进行网格化分,然后利用条件变分法可将其转换为有限元方程:
其中:NE是单元数,
为单元ei上的权函数。n表示边界外法向。通过解方程(7),即可得到Φ的数值解,再由式(2)和式(3)可以求出悬浮区域各点的声压P和振速v,代入式(1)可以求得声场中任一点的U值.计算时取c=340m/s, Vb=4m/s, ρf=1.21g/cm3,谐振频率f=18.6kHz。
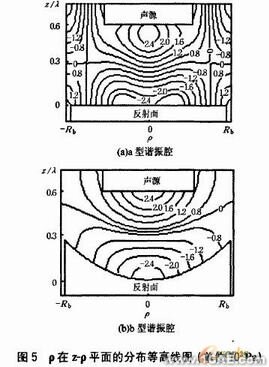
图5是分别采用a, b型谐振腔谐振距离L略大于半个波长时(L≈0.61λ0)模式1下的声压分布等高线图。从图中可以看出,采用两种谐振腔时,其声压分布在轴向都具有声压梯度,这时悬浮样品所处的环境与弹簧振子非常相似,悬浮样品的平衡位置处在声场的悬浮力势阱中,此时样品所受的悬浮力等于重力。当样品从平衡位置下移时,因悬浮力大于重力,会将其向上推;而上移时因重力大于悬浮力,又会被向下压使其回到平衡位置。但是当采用a型谐振腔时,激发出的为平面驻波,声压在径向(ρ向)为常数,不能产生径向定位力,不具有悬浮稳定性;而采用b型谐振腔时,能在径向产生声压梯度,能产生径向定位力,从而可以提高悬浮稳定性。
悬浮样品在声场中所受的悬浮力F为:
由式(8)可以看出,对一给定的声场模式,样品的悬浮位置对应于时间平均势U的极小值。图6是模式1下a,b型谐振腔中U的分布图,(a),(6)为等高线图,(c),(d)为三维图。从图中可以看出,采用a,6型谐振腔时,都能产生一个稳定的悬浮力势阱,“十”表示样品的悬浮位置,但是由于b型谐振腔能够产生径向定位力,使得在相同的激发条件下大大提高了声场强度,从而具有更大的悬浮力。
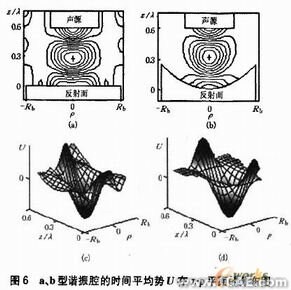
另外,在模式1下进行悬浮实验时,如果先将小球放到凹球面反射面上,经常可以观察到小球在悬浮前不是直接悬浮起来,而是先沿凹球面壁向上滚动到一平衡位置,然后在由该位置自行弹起,从而实现悬浮。对于这一现象,可用以上的模拟结果加以解释。从图6(d)中可以看到,小球在凹球面上时获得的径向力Fp与位移同向。所以在调谐过程中,小球先沿凹球面壁向上运动,当Fp与小球所受支承力的水平分量相等时,小球达到平衡状态。当声场谐振时,小球便由此处直悬浮起来。这说明该声场模型在对悬浮现象预测方面是成功的。
3 结论
(1)声悬浮无容器处理技术是制备高纯物质、研制新材料的一种新型方法,本文研制的单轴式声悬浮装置能实现陶瓷球、钢球等物质的稳定悬浮。
(2)采用有限元方法对两种形状谐振腔的声场进行了数值计算和模拟,结果表明,采用凹球形反射面的谐振腔具有径向稳定性,从而能有效提高悬浮能力。
(3)通过对声悬浮声场时间平均势的分析,解释了在调谐过程中小球沿凹球面壁运动的现象。
相关标签搜索：声悬浮的实验研究及模拟分析 Fluent、CFX流体分析 HFSS电磁分析 Ansys培训 Abaqus培训 Autoform培训 有限元培训 Solidworks培训 UG模具培训 PROE培训 运动仿真
