有限元分析应该注意的那些事

2016-11-10 by:CAE仿真在线来源:互联网

有限元分析应该注意的那些事黄振(山东豪迈化工技术)

引言

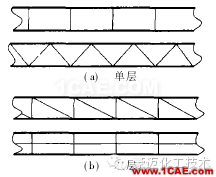
目前有限元应力分析已经成为实施分析设计的重要工具。许多著名的通用有限元软件功能越来越强大、使用越来越“傻瓜化”,只要用户输入一组合理的(但不一定正确的)初始数据,它就能自动地完成计算并输出计算结果,包括直观、漂亮的图形,甚至动画演示。然而,如果所建立的有限元计算模型不能正确反映实际工程结构的特征,或者不能保证有限元计算的精度,输出结果再漂亮也是徒劳无用的。弹性力学基本理论已是久经考验,有限元程序的正确性由软件研制人员和开发商来保证,用户的责任是避免在有限元建模中犯错误。下面从以下几个方面来讨论。1.结构的简化简化能减少计算量,使微机能求解大问题,但简化必须合理。1.1利用局部性局部应力场变化梯度大,网格要加密,但衰减快、影响范围小。整体/局部两次算法:先整体计算,忽略局部细节;再局部计算,以整体计算结果作为边界条件。局部模型的边界应截取到衰减区以外:对小孔(局部结构不连续区),模型边界离小孔边界的距离应大于小孔直径的2倍;对薄壳边缘效应(局部结构不连续区),模型边界离不连续界面的距离应大于。静力分析和动载荷下的疲劳分析局部应力是关键;自振频率计算主要取决于整体刚度与质量分布,局部细节可以忽略。1.2利用对称性、反对称性和周期性

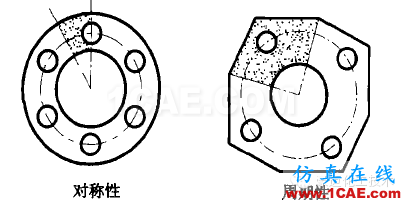
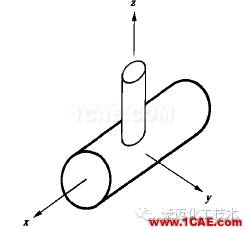
对称性要求几何、载荷、约束条件都对称。反对称性要求几何对称,而载荷、约束条件反对称。轴对称是对同一个轴而言的。管接头中,主管对x轴、支管对z轴都是轴对称的,但管接头整体对x或z轴都是非轴对称的(图2)。对称、反对称和周期条件要给正确。

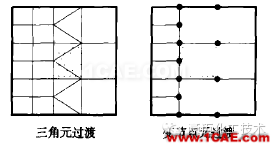
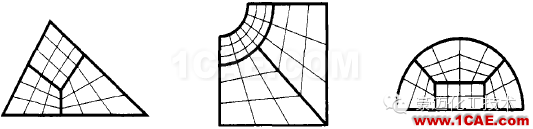
2.单元类型及网格划分2.1单元类型的选定 (1)杆单元只能受拉压;梁单元能受拉、弯、扭; (2)板、壳单元只能计算薄膜应力和弯曲应力,不能计算峰值应力; (3)以四边形及曲边等参元为主,少用三角元,尽量不用退化的三角元; (4)线性单元(二维4节点、三维8节点)内应力均匀分布;二次单元(二维8节点、三维20节点)内应力线性分布,精度好些,网格尺寸约放大一倍,每个单元的计算量较大,总节点数稍小,总计算量偏大。 (5)疏密单元的过渡。利用三角元、变节点元(见图3)。

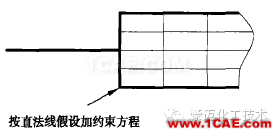
图3疏密单元间的两种过渡方式 (6)板壳元与实体元的连接。按直法线(平面)假设加约束方程(见图4)。

图4板壳单元(左侧)与实体单元 (7)特殊单元的利用。偏置的梁、板、壳单元,例如,板壳的加筋。接触单元,例如,法兰-密封垫片-螺栓系统。垫片单元,可以考虑垫片的迟滞效应。螺栓单元,可以施加螺栓预紧力。层单元,用于纤维增强材料,如玻璃钢,具有正交各向异性,每层铺设方向可以不同,最多100层。2.2网格划分 (1)板壳结构采用实体单元进行模拟时,厚度方向应有4层线性单元或2层二次单元。不合理的方案见图5。 (2)1/4圆弧一般分6~8个单元。 (3)四边形单元的长宽比一般在1∶1到1∶3之间。在板壳结构中,均匀的薄膜应力和弯曲应力区可以取1∶5~7,最多放大到1∶10。 (4)三角形单元的锐角一般不小于30°,最小到15°。四边形单元的最小夹角一般不小于45°。

图5不合理单元示意 (5)应力梯度大的地方网格要加密。在主要的递减(或递增)区间内至少有3~4个单元。 (6)疏密网格的尺寸比一般不大于2。 (7)对尚无经验的算例,需要论证网格尺寸大小的合理性。做基本网格和尺度加密一倍的网格两个算例,若两者计算结果之差在3%~5%以下,则基本网格是可用的。 (8)做热应力分析时,计算温度场的网格应与应力分析的网格相对应。 (9)半自动分元:人工划分大分区,区内自动分元,也得到较规则的网格(见图6)。

图6网格划分示意 (10)全自动分元:选好疏密网格的位置,省事。网格不规则,计算量大,不便于指定校核线的路径。3.边界条件3.1力的边界条件
(1)应力分析报告中不能泛泛地罗列设计任务书中所要求考虑的载荷工况(内压、自重、温度、地震、风载等),而是应该对每一个计算模型如何施加载荷及约束条件作出明确的交待,以备审核。例如,用管(圆柱壳)端等效的轴向均布载荷Peq来代替内压Pi引起的轴向推力时,可按Peq=AiPi/F计算,其中Ai是管内的圆面积,F是管壁的横截面积。该等效载荷计算过程应列入应力分析报告。 (2)集中力下有应力集中。若关心该处应力,应该加密网格,把集中力均摊到3个节点上;若本来是分布力,被简化为集中力,则应通过约束方程要求截面保持平面(见图7);若不关心该处应力,可以只在一个节点上施加集中力,而不考虑该点附近出现的虚假应力集中。

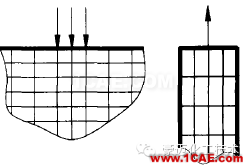
图7力的简化 (3)在均布载荷或温度突变处应设有节点。 (4)在换热器等算例中,基本载荷工况(管程压力、壳程压力、管程温度、壳程温度等)可以加单位载荷来计算,然后乘上实际工况的数值可以组合出多种组合载荷工况。 (5)当压力和温差同时施加时,应根据在一个操作循环中压力和温度随时间变化的曲线来确定最危险工况,最大压力或最大温差点不一定是危险工况。 (6)热分析时应采用金属温度,而不是介质温度。一般设计资料上给的往往是由工艺要求确定的设备内介质的操作温度,由于存在传热过程,结构材料的温度往往不等于介质温度。3.2位移边界条件 (1)约束不足会导致刚体运动。 (2)约束过渡会导致附加应力。图9中的半个卧式容器,对称面限制轴向位移,右端鞍座就不能再固定。 (3)轴对称问题不能限制径向位移,它是靠环向应力与内压相平衡来限制径向变形的。如果限制了,内压就加不上去了(见图9)。 (4)位移边界条件和力边界条件不能重叠。参考文献[1] Kroenke, W C, Classification of Finite Element Stresses Ac-cording to ASME Section III Stress Categories, Pressure Vessels and Piping[J]. Analysis and Computers, New York,NY, 1974·[2] Kroenke, W C, Addicott, G W, and Hinton, B M, Inter-pretation of Finite Element Stresses According to ASME SectionⅢ[J].ASME Paper 75-PVP-Vol.63, 1975.[3] M.W.Lu, Y.Chen, J.G.Li. Two-step Approach of StressClassification and Primary Structure Method[J]. J. Pressure Vessel Technology, 2000,122(1): 2-8.[4]陆明万,陈勇,李建国.分析设计中应力分类的一次结构法[J].核动力工程,1998,19(4):330-337.[5]陆明万.关于应力分类问题的几点认识[J].压力容器,2005,22(08):21-26.

开放分享：优质有限元技术文章,助你自学成才