模态分析方法在发动机曲轴上的应用研究
2016-12-19 by:CAE仿真在线 来源:互联网
综述模态分析在研究结构动力特性中的应用,介绍模态分析的两大方法:数值模态分析与试验模态分析。并着重介绍目前的研究热点一一工作模态分析。通过发动机曲轴的模态分析这一具体的实例,综述了运行模态分析国内外研究现状,指出了其关键技术、存在问题以及研究发展方向。

1.1模态分析的基本概念
物体按照某一阶固有频率振动时,物体上各个点偏离平衡位置的位移是满足一定的比例关系的,可以用一个向量表示,这个就称之为模态。模态这个概念一般是在振动领域所用,你可以初步的理解为振动状态,我们都知道每个物体都具有自己的固有频率,在外力的激励作用下,物体会表现出不同的振动特性。
一阶模态是外力的激励频率与物体固有频率相等的时候出现的,此时物体的振动形态叫做一阶振型或主振型;二阶模态是外力的激励频率是物体固有频率的两倍时候出现,此时的振动外形叫做二阶振型,以依次类推。
一般来讲,外界激励的频率非常复杂,物体在这种复杂的外界激励下的振动反应是各阶振型的复合。模态是结构的固有振动特性,每一个模态具有特定的固有频率、阻尼比和模态振型。这些模态参数可以由计算或试验分析取得,这样一个计算或试验分析过程称为模态分析。
模态分析经典定义:将线性定常系统振动微分方程组中的物理坐标变换为模态坐标,使方程组解耦,成为一组以模态坐标及模态参数描述的独立方程,以便求出系统的模态参数。
模态分析方法主要分三类,分别是试验模态分析EMA、工作模态分析OMA和工作变形分析ODS。
(1)试验模态分析(Experimental Modal Analysis,EMA),也称为传统模态分析或经典模态分析,是指通过输入装置对结构进行激励,在激励的同时测量结构的响应的一种测试分析方法。输入装置主要有力锤和激振器,因此,实验模态分析又分为力锤激励EMA技术和激振器激励EMA技术。
(2)工作模态分析(Operational Modal Analysis,OMA),也称为只有输出的模态分析,而在土木桥梁行业,工作模态分析又称为环境激励模态分析。这类分析最明显的特征是对测量结构的输出响应,不需要或者无法测量输入。当受传感器数量和采集仪通道数限制时,需要分批次进行测量。
(3)工作变形分析(Operational Deflection Shape,ODS),也称为运行响应模态。这类分析方法也只测量响应,不需要测量输入。但是它跟OMA的区别在于,OMA得到的是结构的模态振型,而ODS得到的是结构在某一工作状态下的变形形式。此时分析出来的ODS振型已不是我们常说的模态振型了,它实际是结构模态振型按某种线性方式叠加的结果。
模态分析是研究结构动力特性一种近代方法,是系统辨别方法在工程振动领域中的应用。模态是机械结构的固有振动特性,每一个模态具有特定的固有频率、阻尼比和模态振型。这些模态参数可以由计算或试验分析取得,这样一个计算或试验分析过程称为模态分析。这个分析过程如果是由有限元计算的方法取得的,则称为计算模态分析;如果通过试验将采集的系统输入与输出信号经过参数识别获得模态参数,称为试验模态分析。振动模态是弹性结构固有的、整体的特性。如果通过模态分析方法搞清楚了结构物在某一易受影响的频率范围内,各阶主要模态的特性,就可能预知结构在此频段内,在外部或内部各种振源作用下实际振动响应 。因此,模态分析是结构动态设计及设备故障诊断的重要方法。
近十余年以来,模态分析的理论基础,已经由传统的线性位移实模态、复模态理论发展到广义模态理论,并被进一步引入到非线性结构振动分析领域,同时模态分析理论汲取了振动理论、信号分析、数据处理、数理统计以及自动控制的相关理论,结合自身的发展规律,形成了一套独特的理论体系,创造了更加广泛的应用前景。这一技术已经在航空、航天、造船、 机械、建筑、交通运输和兵器等工程领域得到广泛应用。
1.2数值模态分析与试验模态分析现状及局限性
模态分析过程如果是由有限元计算的方法取得的,则称为数值模态分析;如果通过试验将采集的系统输入与输出信号经过参数识别获得模态参数,称为试验模态分析。两种方法各有利弊,目前的发展趋势是把有限元方法和试验模态分析技术有机地结合起来,取长补短,相得益彰。利用试验模态分析结果检验、补充和修正原始有限元动力模型;利用修正后的有限元模型计算结构的动力特性和响应,进行结构的优化设计。
数值模态分析主要采用有限元法,它是将弹性结构离散化为有限数量的具体质量、弹性特性单元后, 在计算机上作数学运算的理论计算方法。它的优点 是可以在结构设计之初,根据有限元分析结果,便预知产品的动态性能,可以在产品试制出来之前预估振动、噪声的强度和其他动态问题,并可改变结构形状以消除或抑制这些问题。只要能够正确显示出包含边界条件在内的机械振动模型,就可以通过计算机改变机械尺寸的形状细节。有限元的不足是计算繁杂,耗资费时。这种方法,除要求计算者有熟练的技巧与经验外,有些参数〔如阻尼、结合面特征等)目前尚无法定值,并且利用有限元法计算得到的结果,只能是一个近似值 。
试验模态分析是模态分析中最常用的,它与有限元分析技术一起成为解决现代复杂结构动力学问题的两大支柱。利用试验模态分析研究系统动态性能是一种更经济、更有实效的方法。首先,根据已有的知识和经验,在老产品基础上试制出一台新的模型;其次,用试验模态分析技术,对样机作全面的测试与分析,获得产品的动力特性,由此识别出系统的模态参数,建立数学模型,进而了解产品在实际使用中的振动、噪声、疲劳等现实问题;再次,在计算机上改变产品的结构参数,了解动态性能可能获得的改善程度,或者反过来,设计者事先指定好动力特性,由计算机来回答所需要的结构参数〔质量、刚度、阻尼)的改变量。
传统的试验模态分析方法是建立在系统输入输出数据均已知的基础上,利用激励和响应的完整信息进行参数识别。将结构物在静止状态下进行人为激振,通过测量激振力与响应并进行双通道快速傅里叶变换分析,得到任意两点之间的机械导纳函数即传递函数。用模态分析理论通过对试验导纳函数的曲线拟合,识别出结构物的模态参数,从而建立起 结构物的模态模型。根据模态叠加原理,在已知各种载荷时间历程的情况下,就可以预知结构物的实际振 动的响应历程或响应谱。在试验模态分析中大致可以分为四个步骤:1 )动态数据的采集及频响函数或脉 冲响应函数分析;2)建立结构数学模型;3)参数识别; 4)振形动画。与有限元方法相比,结构动力修改的问题在试验模态分析基础上要容易。
传统的模态分析方法已经在桥梁、汽车和航空航天工程等几乎所有和结构动态分析有关的领域中得到广泛应用,数值模态分析与试验模态分析的方法在 理论上已经趋于完善,然而这些方法在具体应用时还是存在局限性,因为对于某些实际工程结构,要获得输入激励的完整信息是难以实现的,或者根本就没有 获得任何输入信息,具体表现为:
1) 海洋平台、建筑物 以及桥梁等在风、浪以及大地脉动作用下引起的振动;导弹以及航天器在飞行运输过程中所产生的振动等,这些结构在实际工作时所承受的载荷往往是不可测量或很难测得,因而无法获得结构系统的激励输入 信息;
2) 某些结构待识别的自由度很多,并且所受载荷的空间分布复杂,往往没有足够的传感器,无法得到完整的输入信息;
3) 所需要的载荷测试量〔力)与能够测试的〔加速度〕不是同一类信号,所需要的量不能直接测试,不能满足识别方法的要求;
4) 很多实际工作中,例如武器结构的振动试验,已经得到大量的振动响应数据,但却没有输入数据。然而目前根据实测振动响应数据往往只能得到诸如共振频率、最大峰 值、总均方根值等特征量,而不能进一步用于对产品 结构的动力特性分析,这就难以对产品的整体变形、响应特性作完整了解,大量的试验结构不能得到充分利用。
针对传统的试验模态分析方法的局限性,发展仅基于响应数据的工作模态分析技术显得尤其重要。采用工作模态分析技术可以避免对输入信息的采集,这样也就解决了传统分析方法中很多状况下输入不可测的问题。
1.3工作模态分析现状及发展趋势
工作模态分析常称为环境激励下的模态分析、只有输出或激励未知条件下的模态分析,正是近年来模态分析领域发展活跃,新理论、新技术的应用层出不穷的一个研究方向,被视为对传统试验模态分析方法的创新和扩展。工作模态分析的优点是:仅需测试振动响应数据,由于这些数据直接来源于结构实际所经受的振动工作环境,因而识别结果更符合实际情况和边界条件;无需对输入激励进行测试,节省了测试费用;利用实时响应数据进行模态参数识别,其结果能够直接应用于结构的在线健康监测和损伤诊断。因此工作模态试验技术使试验模态分析,由传统的主要针对静止结构被扩展到处于现场运行状态的结构,不仅可以实现对那些无法测得载荷的工程结构进行所谓在线模态分析,而且利用实际工作状态下的响应数据识别的模态参数,能更加准确地反映结构的实际动态特性,已经在桥梁、建筑、机械领域取得实质性的进展。
工作模态分析的理论和思想的提出早在20世纪70年代初期就已开始。工作模态的主要手段都是基于响应信号的时域参数辨识技术。随机减量技术最早被用来处理环境激励下的结构响应数据,这一技术 主要是将结构的随机响应转化为结构的自由响应。以此为基础基于时域的辨识方法Ibrahim时域法被提出,极大推动了工作模态分析技术的发展。随着控制理论和计算机技术的发展,多输入、多输出、参数辨识技术也被相继推出,广泛运用的时域模态辨 识方法有多参考点复指数方法、特征系统实现算法等。目前工作模态辨识的其他主要方法还有功率谱密度函数的峰值提取方法、建立自回归滑动平均模型的时间序列分析法、结合时域参数识别的随机减量技术等。
1965年 Clarkson和Mercer提出使用互相关函数估计承受白噪声激励下结构的频响特性,从而提出了当激励未知时使用相关函数替代脉冲响应函数的思想框架。20世纪90年代以来,美国Sandia国家实验 室结合时域模态辨识方法,提出了NExT技术,利用结构在环境激励下的响应的相关函数进行工作模态识别形成上述技术思路后,美国Sandia国家实验室已经将此分析成果成功运用于航天涡轮机、地面载重、 高速公路大桥和濒海建筑的工况信号测量和结构分析中。
在国内,南京航空航天大学振动工程研究所也一直从事着模态分析的研究工作,从传统的模态分析到工作模态分析,也包括只利用响应数据进行系统模态参数识别方法的研究,并且发表了多篇关于环境激励下工作模态参数识别的文章。中国振动协会,上海交通大学振动、冲击、噪声国家重点实验室,哈尔滨工业大学等也致力于研究工作模态参数识别方法。
现有和各种工作模态参数识别方法虽然都有一些很好的应用,但在理论上还需要完善。而且各种工作模态分析方法还有着各自的局限性,如时域法通常要求激励是平稳白噪声,结构系统具有线性时不变特性,其中Thrihim法不易剔除噪声和虚假模态;而时间序列法的模型阶次较难确定;基于响应相关函数的最小二乘复指数法和特征系统实现法要求数据样本长、平均次数多;随机子空间法模型阶次的确定较为繁琐,在测点较多时Hankel矩阵阶次很高,所需要的数据采样量较大。频域法的弊病是要求频率分辨率高、样本长,结构是小阻尼的。时频分析法利用的响应信息太少,是一种局部识别法。
工作模态分析不仅在方法求解上还存在局限性,而且在方法考证中,针对的是较为简单的结构,但即使对于简单结构,现有的方法也不能说解决了所有的问题,当响应测试数据不完整或者测试数据信噪比较低,现有的方法将会遇到困难。同时工作模态识别方法同传统的模态识别方法相比,无论是理论模型、分析手段,还是计算方法都更为复杂,这就可能带来求解上的困难,因此在模型自由度较多时如何保证数值分析的稳定性,是值得进一步考虑的问题。再者如何将它与有限元分析相结合,以获得更加准确的反映结构在实际运行时的动态特性模型,也是目前没有解决的问题。其中的难点在于,现有的工作模态识别方法所得到的振型只是一个相对量,不以质量和刚度阵归一化,同有限元计算结果进行比较有困难。因此工作模态分析的方法还有待于进一步完善。

2.1曲轴模态计算要求
曲轴是一异形转轴类零件,具有轴线不连续、长径比大、结构、复杂等特点,从总体上看,曲轴不是对称或反对称体,对曲轴进行有限元模态分析时必须取整体为研究对象。
根据曲轴的结构形状特点,考虑曲轴的实际使用条件,以有限元计算的数据准备工作量、求解时间及精度等为基本尺度,曲轴模态计算时要求:
(1)曲轴结构形状复杂,建模时应以不影响其结构动特性为简化原则;
(2)有限元模喷网格要有足够的密度,以保证计算结果的精度,真实反映曲轴的模态特性;
对曲轴进行模态分析,求解其前9阶模态。
2.2曲轴模型的简化
曲轴结构形状复杂,小圆角(倒角〉和细油孔(油道〕较多,如果在建模时考虑这些因素则会使有限元模型网格非常密,大大增加数据准备工作最和求解时间,并造成单元形状不理想,求解时累积误差增大,运算精度降低。
在对曲轴进行简化时,参考一些机械结构的模态计算经验,认为小圆角和细油孔对曲轴整体结构动特性影响很小,在建模时忽略半径小于5mm的圆角及直径小于12mm的油道,协调好计算精度与计算工作量之间的矛盾。
2.3曲轴的建模过程
该曲轴由6个连杆轴颈与7个主轴颈组成6个单拐,形成曲轴的主体;第1与第7主轴颈分别向外延伸,形成前端与后端。由于曲轴的很多部分是相似的,所以整体曲轴模型可用子结构模塑组装建立。
本文的曲轴模是在UG中建立的,曲轴的主体模型是根据曲轴的结构特点,先建立一个单拐模型,再通过旋转、平移、合并而成;最后,将主体模型与前、后端模型合并成曲轴的整体模型, 如图1所示。
2.4单元类型的选择
根据曲轴的结构形状特点,结合有限元分析系统的单元库中各种单元的优缺点,选取了求解精度比较卨的10结点单元对曲轴进行模态分析。
2.5单元划分及节点设置
由于只对曲轴作模态分析,综合考虑数据准备最、计算工作量与计算精度,进行网格划分得到:结合点数为89099,单元数为49403。
2.6曲轴有限元模型
将建立的曲轴模型导ANSYS中,进行有限元模型的建立,得到曲轴的有限元模型,如图2所示。


主要是模仿曲轴在磨床上刚刚被夹持的情形,因此要设定曲轴有限元模甩的两端主轴颈圆周面上所有径向位移为零,利用ANSYS中的Block Ianczos法计算并提取出前9阶模态,如表1 所示,前9阶模态振型,如图3~5所示。
表1 曲轴前9阶模态参数
|
阶数 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
频率(HZ) |
169.38 |
181.84 |
397.53 |
472.38 |
513.84 |
760.94 |
796.29 |
832.72 |
917.88 |
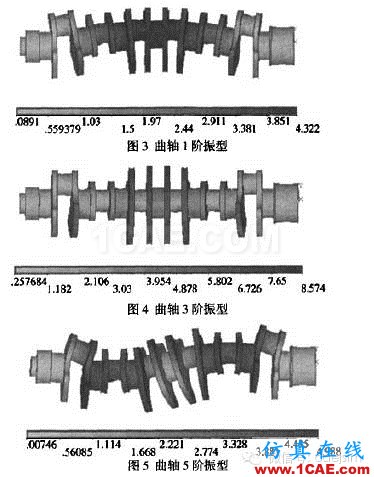
由上面的计算结果和曲轴模态振型可知,在曲轴的前9阶阶次中,其最低的频率为169.38HZ,随着阶次上升,其频率也相应增加。
从图3时以看出曲轴的第1阶模态振型(f=169.38HZ)是曲轴 在垂直平面YOZ和XOZ内的一弯振动;从2阶振铟图(图略〉可以看出,曲轴的第2阶模态振型(f=181.84HZ)是曲轴在平面YOZ和 XOZ内的一弯振动;从振型图4可以看出,曲轴的第3阶模态振型 (397.53HZ)是曲轴在XOZ平面内的一弯振动,第三缸和第四缸变形最大;从4阶振型图可以看出,曲轴的第4阶模态振型(f=472.38HZ)是曲轴在平面YOZ和 XOZ内的二弯振动,第三缸和第四缸变形最大;从振型图5可以看出,曲轴的第5阶模态振型(f=513.84HZ)是曲轴在平面YOZ内的二弯,以及在平面XOZ内的 二弯振动;从6阶振型图可以看出,曲轴的第6阶模态振型(f=760.94HZ)是曲轴在平面YOZ内的二弯振动,以及Z向的振动。 由于曲轴在第7阶、8阶、9阶的振型变化相对前几阶要小,所以在这里就不再详细叙述。总体来看,在曲轴的9阶模态振型中,变形最大基本上都出现在第三和第四缸,以及他们之间的连杆轴颈处。
通过上面曲轴的有限元模态分析,从振型图上可以看出,曲轴的低阶频率下主要以弯曲振动为主,并且弯曲变形最大的部位出现在连杆轴颈与曲柄臂和平衡块的结合处。由此可预见,弯曲裂纹是最容易出现在这些地方的。

数值模态分析与试验模态分析是目前研究结构动力学特性的两大方法,已经成为解决现代复杂结构动态特性设计的相辅相成的重要手段,在以后的研究过程中,它们在应用领域会得到进一步的发展。
工作模态分析作为目前模态分析领域中一个研究热点,尽管存在某些不足,但由于它所固有的、在工程应用上的巨大前景和优势,以技术创新和发展为基础,相信工作模态技术将会有更加广泛的发展和应用。
相关标签搜索:模态分析方法在发动机曲轴上的应用研究 有限元技术培训 有限元仿真理论研究 有限元基础理论公式 能量守恒质量守恒动量守恒一致性方程 有限体积法 什么是有限元 有限元基础知识 有限元软件下载 有限元代做 Fluent、CFX流体分析 HFSS电磁分析 Ansys培训






