结构分析：稳定与静定判断

2017-05-05 by:CAE仿真在线来源:互联网

两个基本假设,除非特殊注明,否则都是在这两条假设的范围之内。

第一条是「小变形」,也就是意味着忽略二阶变形。比如一根悬臂梁,端头受竖向荷载作用,悬臂梁向下弯曲。事实上,自由端不仅在竖向有变形,在水平向同样也有变形。但水平变形与竖向变形相比,实在是太小,所以可以忽略。也就是,悬臂梁的自由端近似可以看作直上直下的位移,没有水平方向的二阶变形。

第二条是「线弹性」,也就是可以使用叠加原理。比如一根简支梁,跨中承受集中荷载 P,产生的竖向位移为 Δ;如果再叠加上一个 P,则位移也会相应的增加一个 Δ。并且,这跟一开始就直接施加一个 2P 的效果是一样的,同样造成 2Δ 的跨中位移。

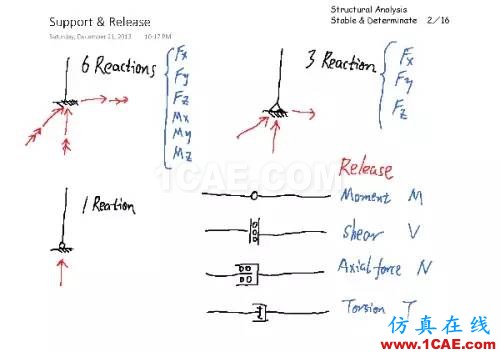
三种基本的支座:fix support 固定支座,在三维空间在有6个支座反力,限制了三个方向的移动和转动;pin support 铰接支座,3个支座反力,限制了三个方向的移动,但没有限制三个方向的转动;roller support 链杆支座,只限制了一个方向的移动。事实上,还有很多其它支座,空间6个自由度,可以排列组合出很多种支座形式,比如滑动支座、两个链杆组成的支座等等。

对应于四种内力形式,我们有四种杆端释放,分别是弯矩释放、剪力释放、轴力释放、扭矩释放。也就是,这个释放的部位不能传递相应的弯矩、剪力、轴力、扭矩。最简单的例子,剪刀中间的那个转轴,就无法传递弯矩,把剪刀平放在桌面上,假设它运转良好,没有生锈,那么你转动剪刀的一部分,无法让另一部分跟着转动。

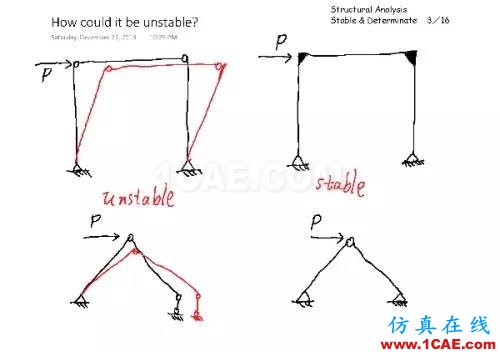
我们的主要目的是判断结构是否稳定。什么是稳定呢?比如左上图,就不稳定,轻轻一推,它就从矩形变成平行四边形了;相应的,右上图是稳定的,因为你推它,它已经不会变成平行四边形了,而是能够有效的保持自己的几何形状。

同样的,左下图这个也不稳定,因为你一推它,它就自己趴下去了,右边的支座会向右滑动;而右下图则是稳定的,右支座不会发生水平滑动,整个体系不会发生刚体移动和转动。

除了判断稳定与否,另一个重要的结果就是要判断静定与否。基本的流程:第一步先计算未知数的数量 #un 和存在的方程的数量 #eq。然后判断两者的大小,如果 #un 比 #eq 小,则结构不稳定;如果 #un 大于等于 #eq,则判断结构体系是否会发生整体或者局部的刚体移动和转动,换言之,是否稳定;如果会发生刚体位移,则结构不稳定;如果结构稳定,则继续判断是否静定,如果 #un 等于 #eq,则结构静定,如果 #un 大于 #eq,则结构超静定。

比如一根简支梁,未知数的数量为6,分别是3个支座反力、梁的3个内力(轴力、剪力、弯矩);存在的方程的数量也是6,分别是2个节点的水平力平衡、竖向力平衡、弯矩平衡。整体体系和局部都不会发生刚体位移,所以是稳定结构;#un 等于 #eq,所以是静定结构。

对于平面桁架,未知数的数量 #un 等于 1m+r,也就是每根杆件1个未知量(轴力),外加所有的支座反力;方程式的数量 #eq 等于 2j,也就是每个节点2个方程(水平力平衡、竖向力平衡)。

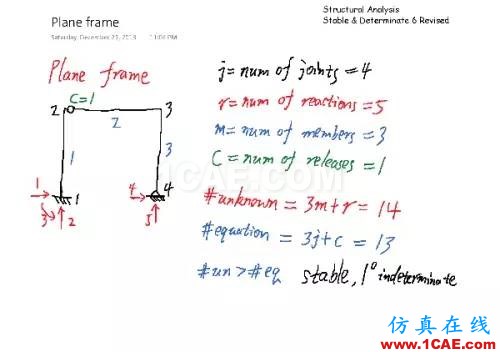
对于平面框架,未知数的数量 #un 变成了 3m+r,也就是每根杆件3个未知量(轴力、剪力、弯矩),外加所有的支座反力;方程式的数量 #eq 等于 3j+c,也就是每个节点3个方程(水平力平衡、竖向力平衡、弯矩平衡),外加每个内力释放位置的1个方程(该点被释放的该项内力等于0)。

空间桁架,未知数的数量 #un 仍然是 1m+r,每根杆件1个未知量(轴力),外加所有的支座反力;方程式的数量 #eq 则变成了 3j,也就是每个节点3个方程(x方向力平衡、y方向力平衡、z方向力平衡)。

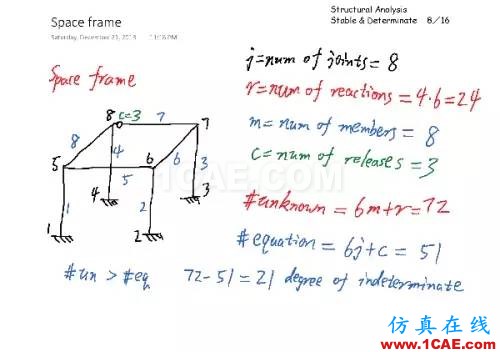
空间框架,未知数的数量 #un 是 6m+r,每根杆件6个未知量(轴力、y向剪力、z向剪力、y向弯矩、z向弯矩、扭矩),外加所有的支座反力;方程式的数量 #eq 则等于6j+c,也就是每个节点6个方程(x、y、z 方向力平衡,x、y、z 方向弯矩平衡),外加每个内力释放位置的1个方程(该点被释放的该项内力等于0)。

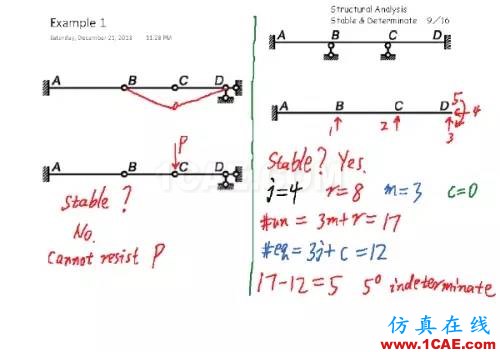
左边的例子,看上去挺「稳定」,但其实并不稳定,它无法承担施加在 C 点的竖向荷载,整个体系没有内力和支座反力能够跟这个外荷载平衡。

右边则是一个稳定结构的例子,未知量的数量是17,方程的数量是12,所以是5次超静定。换言之,我适当的删去5个约束,这个结构就变成了一个静定结构,也就是图中的悬臂梁。

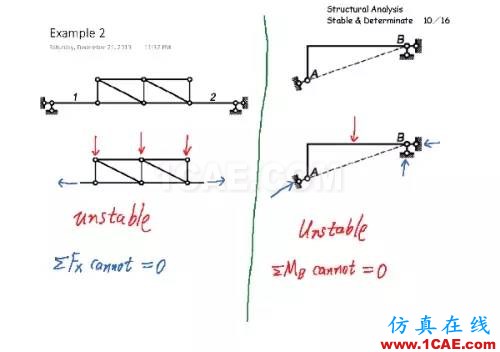
左边的这个桁架之所以不稳定,是因为它无法把竖向荷载传递到支座。如果我们取图中所示的隔离体,两侧被切断的杆件只有水平向的轴力,没有可以与外荷载平衡的竖向内力。

右边的这个同样不稳定,因为它的三个支座反力都经过B点,也就是对B点的弯矩为0。整个系统的支座反力无法和外荷载造成的B点的弯矩平衡。

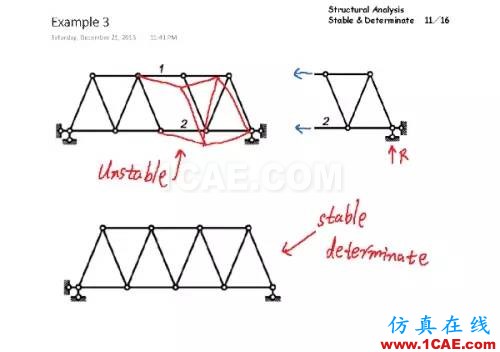
这个桁架不稳定是因为它的1、2杆件无法传递竖向荷载,如果我取右侧的隔离体,左侧被切断的杆件没有竖向内力跟支座反力平衡。换言之,1、2杆件之间的这个平行四边形会发生刚体形变。

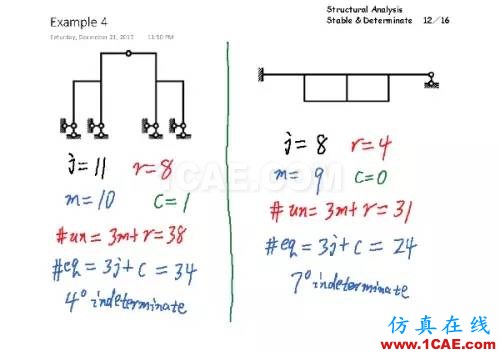
这两个平面框架都是稳定结构,左边的超静定次数是4,右边的是7。

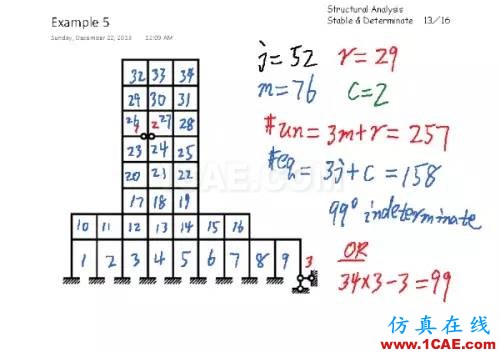
这个框架同样是稳定结构,超静定次数是99。我们可以用 #un 和 #eq 来计算超静定次数,也可以用简便方法,数格子的数量,每个格子的横梁提供了3个额外约束,格子的数量乘以3,再减去缺失的约束的数量,就是总的超静定次数。

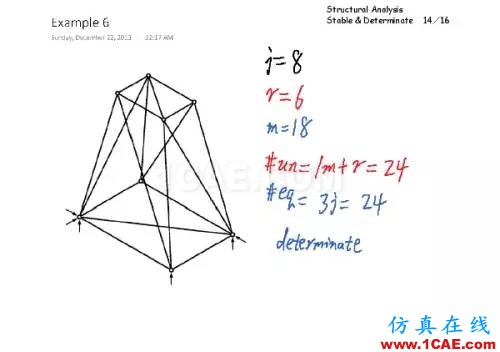
这是个空间桁架的例子,稳定,静定。

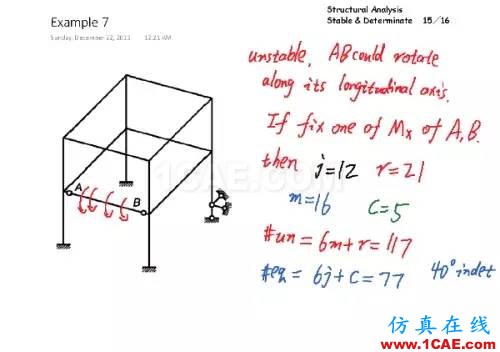
空间框架的例子。如果 A、B 两点同时释放了各自的3个方向的弯矩,则 AB 杆件可以绕着自己的长轴旋转,所以结构是不稳定的。如果固定了 A 的扭矩,限制住 AB 杆件绕自己长轴的旋转,则结构变为稳定结构,40次超静定。或者,共有8根横梁,每个横梁提供了6个额外的约束,8乘以6等于48,再减去 A 释放的2个约束、B 释放的3个约束、右下角支座释放的3个数月,就等于40个额外约束,也就是40次超静定。