流体运动的拉格朗日描述和欧拉描述及声波方程

2017-02-27  by:CAE仿真在线  来源:互联网

摘要:拉格朗日描述与欧拉描述乃描述流体运动的两种体系。两种描述对于线性声学几无分别,但对非线性声学则不然。人们或惯用欧拉描述分析求解声学问题,但对有些非线性问题若采用拉格朗日描述更直接了当,更易求得解析解。本文概论概述两种描述,探讨拉格朗日描述下流体运动的基本方程,最后给出一维的非线性声波方程。

何谓拉格朗日描述和欧拉描述?

欲描述流体的运动,既可选择拉格朗日坐标体系,也可采用欧拉坐标体系。拉格朗日描述取初始时刻(如时间t=0)流体质点的三维位置矢量R=(a,b,c)作为空间变量,并标记该流体质点。随着流体的运动,t时刻的质点运动至新的三维空间位置r=(x,y,z)。显然,r与R具有函数关系:r=r(R,t),或用笛卡尔坐标分量表示

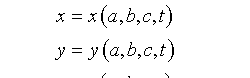
该关系其实给出了流体质点在空间的运动轨迹。由此可求出质点运动的速度——流速v。

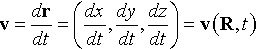
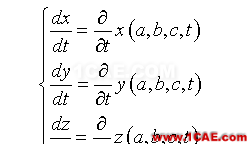
显然,不同的质点具有不同的速度,即流速v不但是时间的函数,也是初始位置R的函数。不仅如此,任何描述流体状态的物理量(例如密度ρ)均属流体质点所“携带”的。不同质点的运动状态当然不同;故流体的任何物理量不仅是时间t的函数,也是初始坐标矢量R的函数,例如,密度ρ=ρ(R,t)。此种以流体质点初始位置R和时间t描述流体运动的方法,即所谓的拉格朗日描述,其中R=(a, b, c)是拉格朗日坐标。其实,拉格朗日坐标相当于质点的“标签”。所以,拉格朗日描述记录了质点的时间演化,既可追溯质点的既往,也可预测质点的未来。

与一般的流动不同,声学问题中的质点运动是围绕初始位置R=(a, b, c)的质点振动。记振动位移矢量为δr=(ξ,η,ζ),则r=R+δr,或者,

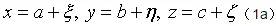
当然,位移δr也是初始位置R=(a, b, c)和时间t的函数:δr=δr(R, t),或用分量表示:

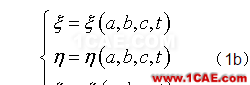
与拉格朗日描述不同,欧拉描述乃现实主义的描述手法。它仅关注“现在”——t 时刻处于空间r=(x,y,z)位置的质点。在此描述下,所有物理量皆表为空间位置坐标r(欧拉坐标)和时间t的函数,例如密度ρ=ρ(r,t)。所以,欧拉描述所描绘的是流场在不同时刻的瞬时空间分布,其空间坐标r=(x,y,z)是纯数学的独立变量。

两种描述的关系

虽然如此,t 时刻位于空间位置r=(x,y,z)的流体质点并非“空穴来风”,而是从别处迁移而来。运动规律r=r(R,t)或公式(1)可对质点“追根溯源”:原则上,根据当前的空间位置r反推初始位置R。据此,欧拉描述和拉格朗日描述可以相互转换。为明确起见,特以上标(L)和(E)分别标记拉格朗日和欧拉体系下的物理量,例如密度ρ(L)(R,t)和ρ(E)(r,t)。据上论述,

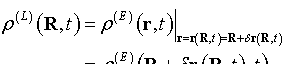
诸如声波这般流体运动,位移δr的量值一般很小(即,δr的范数||δr||<<1),因此可以对上式右端作泰勒展开:

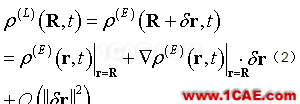
式中,欧拉空间的梯度算符:

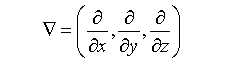
可见,已知位移δr=(ξ,η,ζ),就可从欧拉体系的物理量求得拉格朗日体系的对应量。反之,若函数r=r(R,t)连续可逆,可求得逆函数R=R(r,t),从而可把拉格朗日体系的物理量转换为欧拉体系的【注1】。特别是,对于小位移振动的情形,有如下展开

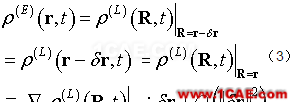
式中,拉格朗日空间的梯度算符

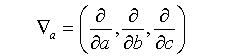
可见,拉格朗日描述的物理量ρ(L)(R,t)与欧拉描述的ρ(E)(r,t)仅相差量级O(||δr||)。

数学上,函数关系r=r(R,t)或公式(1)所表达的是以时间t为参变数的空间映射:

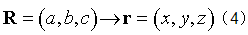
矢量r在拉格朗日空间的梯度:

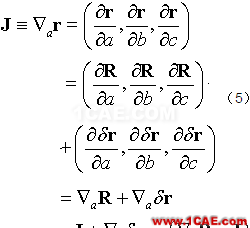
是一个“矢量的矢量”——张量,刻画了映射的性质,式中I是单位张量。J也可用等价的雅可比矩阵形式表示:

式中的下标表示对相应变量(a,b,c)的导数,例如:

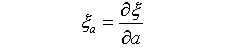
连续性方程

设某质点的初始体积ΔV0(→0),t 时刻的体积ΔV。根据数学分析,雅可比矩阵J的行列式(记为|J|)是在映射(4)下质点体积元的缩放因子:

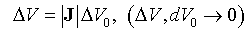
设流体初始的质量密度为ρ0,t时刻的质量密度为ρ。根据质量守恒定律,ρ0ΔV0=ρΔV。将上式代入,得到拉格朗日坐标下的连续性方程

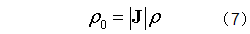
对于一维的情形,根据定义(6)知|J|=1+ξa,公式(7)遂简为:

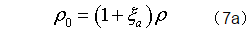
运动方程

理想流体的运动遵循欧拉方程:

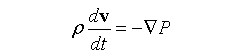
式中,P是流体压强。在拉格朗日体系中,速度v也是拉格朗日坐标R=(a,b,c)和时间t的函数:v = v(R, t)。所以,加速度dv/dt是对v的时间偏导数。如此,上列欧拉方程可改写为

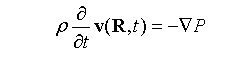
在此方程的等式两端同时点乘矢量:

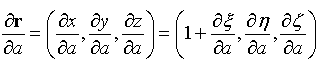
并利用微分关系

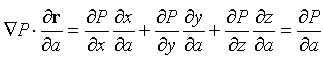
得到

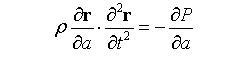
同理,可得

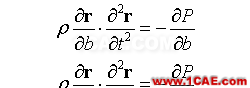
三个方程合而为一,可表为

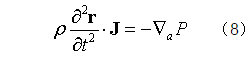
此即拉格朗日体系的流体运动方程。式中,雅可比矩阵J由公式(6)给出。或者,利用公式(5)用位移矢量δr表示,

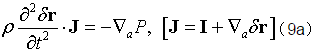
如以矩阵表示,则可表为矩阵形式

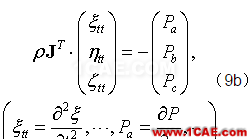
在一维情形,J = 1+ξa,方程(8)于是简化为:

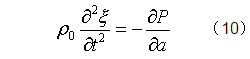
其中已经利用了连续性方程(7a)。可见,拉格朗日描述下质点的一维运动方程是线性的。当然,质点运动仍是非线性的,集中体现在连续性方程(7)以及(下述的)状态方程中。

一维理想流体的非线性声波方程

理想流体(如气体)满足绝热状态方程:P=P(ρ)。利用连续性方程 (7a),则:

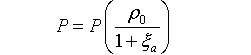
代入一维运动方程(10)的右端,得到非线性声波方程

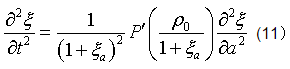
其中P'(ρ)=dP/dρ。如果|ξa|<<1,则可对方程(11)作线性化处理,从而得到熟知的线性波动方程。若|ξa|<1,则有泰勒展开:

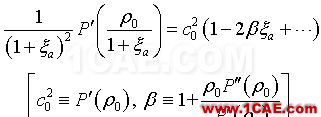
式中,c0是熟知的线性声速,而β是非线性系数,衡量媒质本身(二次)非线性的大小。若仅计及二阶非线性小量,则方程(11)可近似为

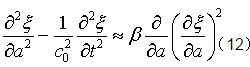
方程的左端是标准的一维波动方程,而右端的非齐次项是二次非线性的贡献。

---

【注1】在诸如湍流等复杂流动情形,可逆性或许不存在,两种描述难于转换。

本文来源于网易聲之韻博客,作者王新龍,南京大学声学研究所。

相关标签搜索：流体运动的拉格朗日描述和欧拉描述及声波方程 CFD培训 CFD流体分析培训 cfd视频 fluent cfx pumplinx软件培训 Fluent、CFX流体分析 HFSS电磁分析 Ansys培训 Abaqus培训 Autoform培训 有限元培训