基于HyperWorks对重汽鞍座连接板的优化设计

2017-02-15 by:CAE仿真在线来源:互联网

摘要:建立了重汽鞍座连接板的有限元模型,结合OptiStruct以体积比为约束目标进行了拓扑优化,根据优化后连接板形状得到优化设计方案。通过拓扑优化,减轻了鞍座连接板的重量,节约了材料,且满足强度要求,缩短了研发周期。通过试验结果证明,本文所建有限元模型是合理有效的。

1概述

在重汽鞍座连接板的设计过程中,利用优化方法可以在结构满足强度、刚度的前提下,通过改变某些设计变量,使结构的重量最轻,节约材料,缩短研发周期。

重汽鞍座连接板优化主要结合AltairOptiStruct结构优化平台,在线性分析过程中考虑拓扑优化。利用给定的设计空间,采用拓扑优化,在较短的时间内,寻求最佳材料分布,得到一个优化设计方案,计算表明本方案不但满足部件的刚度、强度要求,并且其最大应力、应变都没有超过材料的最大屈服强度。

2鞍座连接板有限元模型

根据设计人员提供的三维模型,在HyperMesh中建立有限元模型。建模过程中,出于计算经济性考虑,在不影响整体刚度、强度的前提下,对模型进行部分简化,最终建立重汽鞍座连接板的有限元模型如图1所示:

图1重汽鞍座连接板有限元模型

3拓扑优化模型建立及分析

拓扑(Topology)优化是一种优化方法,能在给定的空间结构中生成优化的形状及材料分布。通过将区域离散成有限元网格,OptiStruct为每个单元计算材料特性,在给定的约束条件下,利用OptiStruct中的优化算法更改材料的分布,以优化用户给定的设计目标,当目标函数在任意连续三次迭代中的改变量低于给定容差时,即得到收敛结果。

优化的数学模型[1]可以表述为:

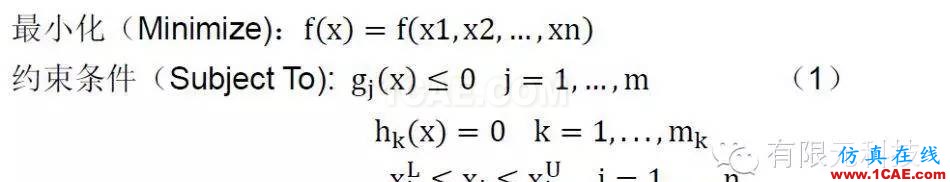
式中,X =x1,x2,. . . ,xn是设计变量;f(x)是目标函数;g(x)是不等式约束函数;h(x)是等式约束函数,上角标L是指LowerLimited,即下限;上角标U是指Upper Limit,即上限。

在OptiStruct中,目标函数f(x)、约束函数g(x)与h(x)是从有限元分析中得到的结构响应。设计变量X的选择依赖于优化类型。在拓扑优化中,设计变量为单元的密度。

在HyperMesh中建立的有限元模型,设定相应的设计目标,约束条件和设计变量,采用OptiStruct进行拓扑优化。经过4次迭代得到优化结果,得到最优拓扑结构见图2所示。

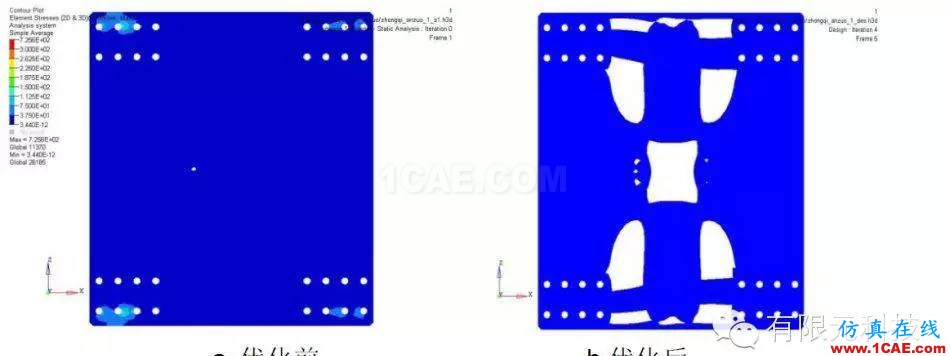
基于HyperWorks对重汽鞍座连接板的优化设计hypermesh应用技术图片3

图2重汽90鞍座连接板优化结果

由图2可见,优化后的鞍座连接板相比优化前节约材料,重量变轻。

4鞍座连接板应力计算与验证

本文对鞍座连接板优化前后的应力进行比较验证。鞍座连接板在弯曲、扭转工况下,在前后钢板弹簧上施加约束,在鞍座的两个支撑上分别施加垂直向下的集中载荷以及牵引车与半挂车之间的纵向牵引力,如图3所示。垂直载荷大小都取250KN,纵向牵引力都取76KN。

基于HyperWorks对重汽鞍座连接板的优化设计hypermesh应用技术图片4

图3约束、加载位置

优化前后弯曲、扭转工况下的应力略有增加,但都没有超过材料的屈服强度,应力分布如图4所示。

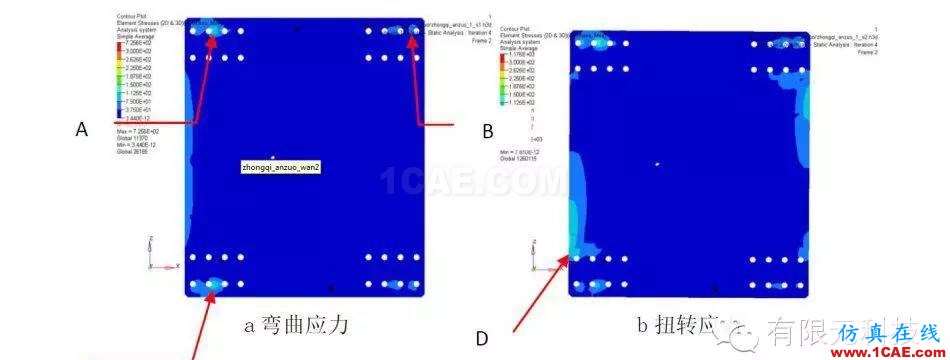
基于HyperWorks对重汽鞍座连接板的优化设计hypermesh应用技术图片5

图4弯曲扭转应力图

鞍座最终优化后应力分布对比见表1。

基于HyperWorks对重汽鞍座连接板的优化设计hypermesh应用技术图片6

表1应力对比图(单位:Mpa)

将最终优化结果利用OptiStruct软件包中的OSSmooth工具,生成IGES格式的文件,设计人员输入到

CAD系统中进行二次设计,最终得到连接板形状如图5所示:

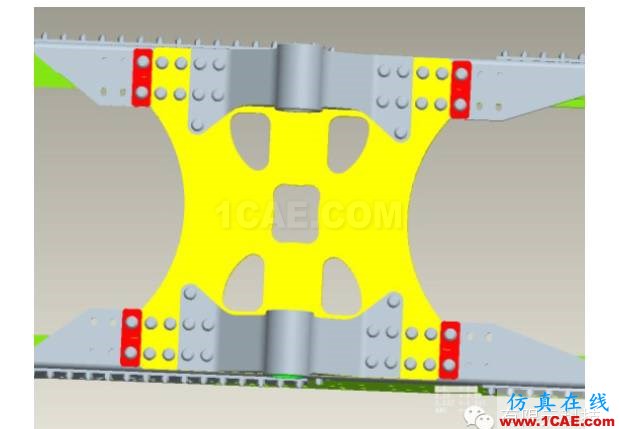
基于HyperWorks对重汽鞍座连接板的优化设计hyperworks仿真分析图片7

图5连接板

5结论

本文建立了重汽专用90鞍座连接板的有限元模型,根据优化目标对连接板建立了拓扑优化模型,通过设定优化目标,对连接板进行优化,得到了最优形状,并通过设计人员对优化形状进行细化,最终减重约22.5公斤,并已通过400万次的垂直载荷16吨至48吨以及200万次的32吨至48吨的台架试验,均未出现任何问题,满足设计要求,且已进入路试阶段。优化结果与试验验证表明,利用拓扑优化得到的结果是合理的,在满足鞍座连接板的设计要求以及强度要求的条件下,达到了减重目的。

开放分享：优质有限元技术文章,助你自学成才