双螺杆几何参数设计(2)- 同向旋转双螺杆
2017-05-13 by:CAE仿真在线 来源:互联网
对紧密啮合同向旋转双螺杆来说,两螺杆中心距、螺杆直径、螺纹头数以及螺纹顶角之间存在一定的关系,不可随意设计,否则两螺杆之间会发生干涉。本文从两螺杆的同向运动轨迹出发来讨论同向旋转双螺杆理论端面曲线形成以及双螺杆的三维实体造型。
一、啮合原理
对于无间隙紧密啮合同向旋转双螺杆,两螺杆旋转速度相同,方向也相同,如图1所示。设想从螺杆圆柱体上切下两个与其轴线垂直的盘形断面1和2,固定盘形断面1,盘形断面2围绕着盘形断面1作圆形移动。圆心C0围绕圆心O,以OC0为半径沿着圆形轨迹移动,盘形断面2本身就不作任何旋转运动,因此盘形断面2上的各点同样以相同的半径沿圆形轨迹运动。若盘形断面2圆周上、中间带有点P3和P4的弧P1P2为螺棱的话,如图1所示,弧上各点就沿中心在盘形断面1圆周上且与该点水平距离为Cl、半径为Cl的弧线运动。所有这些点组成的这组弧线从盘形断面1上切去一个半月形的部分F,被切去部分F的形状与垂直于旋转轴线的螺槽断面形状一致。
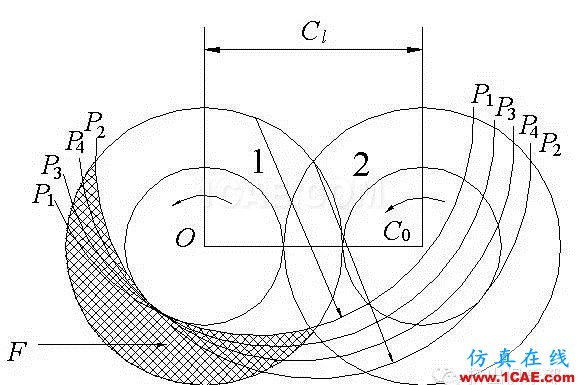
图1同向旋转双螺杆的啮合原理
二、横截面几何形状的形成
对于一给定螺杆直径Ds、中心距Cl、螺纹头数ns的紧密啮合同向旋转双螺杆,由于每根螺杆的螺棱在旋转过程中都要与另一根螺杆相啮合,因此根据相对运动原理,可用图形方式求出其横截面形状。首先用一对单头、给定中心距Cl和螺杆外径为Ds的双螺杆来描述其横截面的形成。
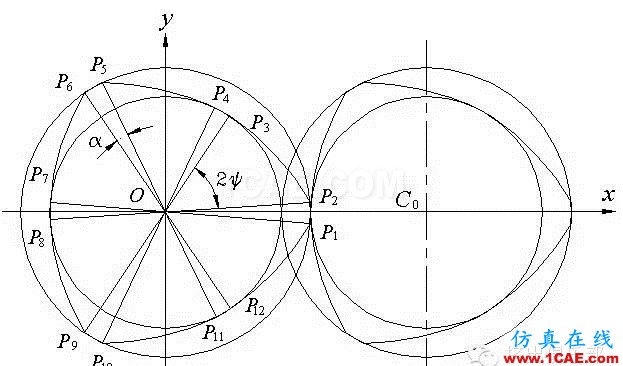
在图2中,设PQ是盘B的螺棱,要确定与B盘螺棱PQ相啮合的盘A螺棱的形状,必须绘制PQ相对于盘A的运动轨迹。两个圆盘起初都以速度ω顺时针旋转,当我们对系统加一个绕A盘中心O点作速度为ω的逆时针旋转运动时,盘A就静止了,盘B中心C0绕O点以ω速度逆时针旋转,其轨迹为以O为圆心,半径为Cl的一个圆,同时盘B也停止了绕其中心C0的旋转运动,也就是说盘B绕盘A的中心O点作圆平动。
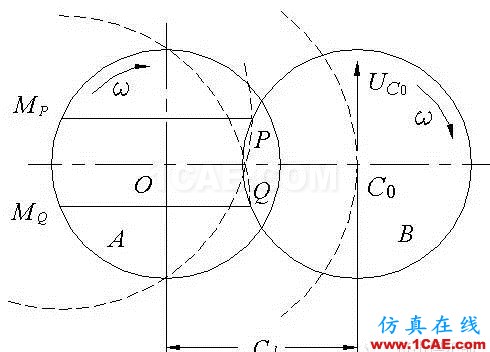
图2同向旋转双螺杆点P、Q轨迹分析
在相对运动中,盘B不绕其中心C0旋转,因此B盘上所有点的运动轨迹都是半径为Cl的圆。在图2所示位置中,C0的相对速度是垂直于水平轴的,B盘上任意点在这一时刻的速度都垂直于水平轴,因而P点的运动轨迹的中心为MP,在通过盘A螺棱的圆上。同样,Q点运动轨迹的中心MQ也在通过盘A螺棱的圆上。
图3表示了螺棱PQ相对运动中的不同位置,C1、C2是特定的点,使直线C1Q1和C2P1通过O点。当B盘中心C在C1和C2之间时,盘A的轮廓形状是由圆弧PQ“扫过”形成的;在这一个区间外,盘A螺棱形状是由P、Q的轨迹形成的。圆弧顶端PQ作圆平动时,在A盘上形成的轨迹为圆弧Q1P1,其圆弧半径Rr为:Rr=Cl-Rs,当B盘中心C在C1、C2之间移动则可得到圆弧Q1P1,角Q1OP1等于顶角。因而,在A盘上的无间隙啮合轮廓曲线就可由圆心为O点、半径为螺槽底部半径Rr的圆弧Q1P1,圆心分别为MP、MQ半径均为Cl的P、Q点的轨迹圆弧以及圆心为O点、半径为螺棱顶部半径Rs的四段圆弧组成。
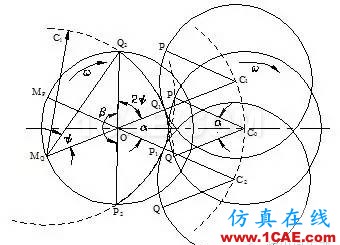
图3 A盘螺棱形成原理
在绘制图3的螺杆横截面曲线时,并没有强调两根螺杆必须有相同螺纹顶角,图3画出了单头螺纹螺杆A盘的顶角远大于B盘顶角的螺棱形状。根据两螺杆互不干涉原理,A盘的根角Q1OP1和B盘的顶角必须相等,同样,A盘的顶角和B盘的根角也应相等。为进一步讨论具有相同顶角和根角的两圆盘的横截面形状,引入啮合角∶
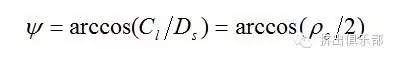
定义中径比为中心距Cl与螺杆半径Rs的比,是无量纲参数。图3中,角Q1OQ2是2倍的啮合角,因而绕O点对各角求和,可得∶
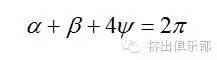
对于单头螺纹对称横截面时的情况,顶角为∶
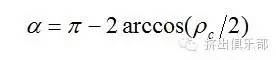
对于ns头螺纹,上式变为∶
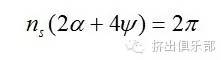
将啮合角定义式代入上式,可得中径比与螺纹顶角的关系∶
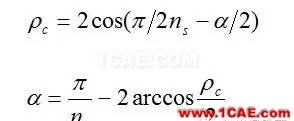
由于螺棱具有一定的厚度,因此螺棱顶角必须大于零,由上式可知,中径比不可随意设计,有一定限制,其下限为∶
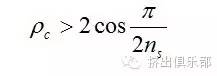
对于无间隙啮合两螺杆,其螺槽深度h∶
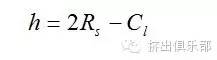
而且槽深也必须大于零,可得中径比上限∶
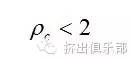
由中径比上下限可得中心距Cl取值范围∶
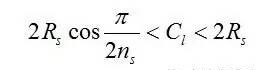
为形象起见,在图4中画出了ns=1、2、3时,B盘对A盘作相对运动时,在24种不同位置形成的报络线形状,A盘的螺棱形状为B盘的内包络线。
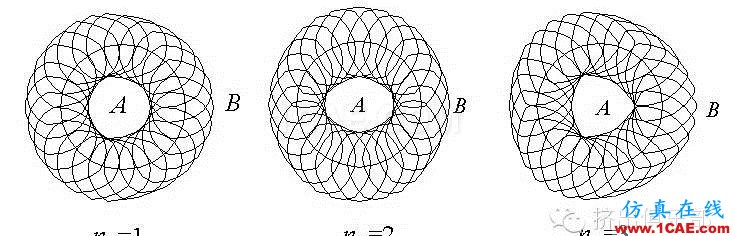
图4两螺杆作相对运动形成的包络线
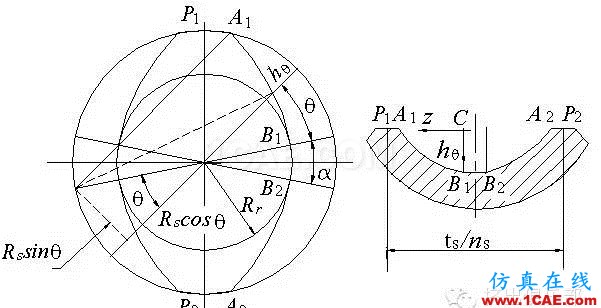
图5双头螺纹螺杆的截面形状(左为横向截面形状,右为纵向截面形状)
图5给出了垂直于螺杆轴线的横截面图和通过螺杆轴线的轴截面图。点P1、P2在相邻两螺棱的中心线上,轴向距离为ts/ns,或者相邻两螺棱的夹角为2Pi/ns弧度。B1B2为螺槽底部,线段B1B2距离为螺棱宽度,Theta为以螺杆根角为起点的任意圆周角(单位为弧度),C点与B1点垂直距离为螺槽深度h。螺槽深度在B1B2之间是常数,在B1和A1之间是Theta的函数。在C处我们引入z轴坐标原点,则z与Theta的关系为∶
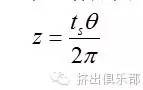
螺槽深度为∶
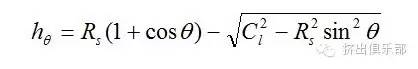
将z的表达式代入上式可得槽深q和z的关系∶
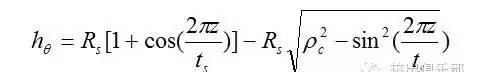
从图5可以得出B1B2轴向距离为∶
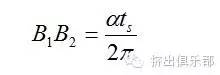
因而通过轴线平面内的螺槽横截面形状就由Rs、槽深和B1B2所决定。
三、三维实体造型
计算机技术的发展,为螺杆设计提供了有力的工具。在设计初期,可以对所选参数进行螺杆三维实体图形显示,检验所选几何参数的合理性。
双螺杆的几何参数直径Ds,中心距Cl、螺纹头数ns、以及导程ts一般都可按工作条件预先给定,从而求出横截面几何形状。为绘制三维图形,首先需给出横截面上几个关键点的坐标值,以便画出螺杆横截面图形。
下面讨论ns=1、2、3时螺杆横截面曲线上各关键点(各段圆弧的起始点)的坐标值。
1.单头螺纹元件
如图6,建立直角坐标系xoy,Ds、Rs、Rr、Cl、ns、ts都已知,其啮合角和螺纹顶角为:

点P1、P2、P3、P4坐标值为∶

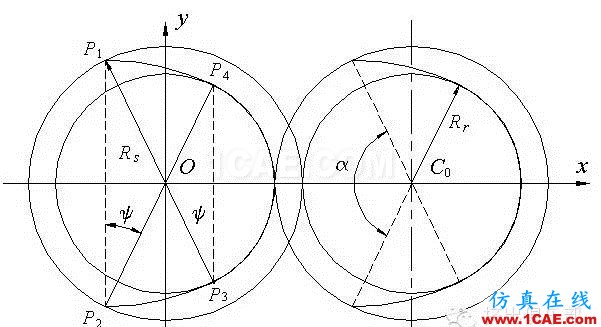
图6ns=1螺纹横截面形状
由图6还可看出,对于单头螺纹元件来说,其横截面曲线由四段圆弧组成∶P1P2、P2P3、P3P4、P1P4,在常用三维造型软件中利用画弧命令就可以画出这些圆弧。
2.双头螺纹元件
已知∶Ds、Cl、ns=2、ts
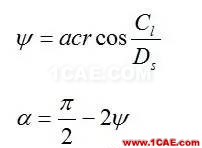
从图7中,可以得出横截面上关键点和圆弧圆心的坐标,利用画弧命令可将螺纹端面形状画出。
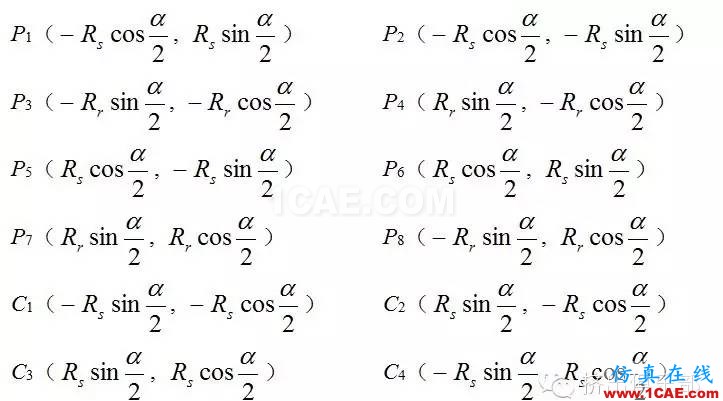
图7ns=2螺纹横截面形状

3.三头螺纹元件
如图8,三头螺纹元件螺纹端面各关键点和圆弧中心的坐标如下∶

图8ns=3螺纹横截面形状
于上述螺纹元件的横截面几何形状,用画弧命令就可将整个端面画出。在三维实体造型软件,如UG、SolidWorks中绘制出端面曲线后,再画一条直径为螺杆外径、导程为螺杆导程的空间螺旋线,利用扫掠命令就可以将螺杆横截面沿此螺旋线作向z轴的扫掠,形成螺杆的三维实体造型。最后,用拷贝命令得到另一根螺杆,对其中一根作相应的旋转,就得到同向双螺杆的真实的三维实体。可以对实体模型进行干涉检查、剖面处理和动画处理,并可获得一系列数值信息(如螺棱宽、面积、体积)和设计加工刀具所需的螺杆轴向、法向截面形状。图9就是用三维软件制作的无间隙紧密啮合的同向旋转双螺杆三维实体图。

图9同向旋转双螺杆三维实体图(ns=3)

相关标签搜索:双螺杆几何参数设计(2)- 同向旋转双螺杆 机械设计培训 机械设计课程 机械设计视频 机械设计技术教程 机械设计资料下载 SolidWorks UG inventor软件应用 Fluent、CFX流体分析 HFSS电磁分析 Ansys培训 Abaqus培训






