莫比乌斯转环_组件动画
2017-09-11 by:CAE仿真在线 来源:互联网
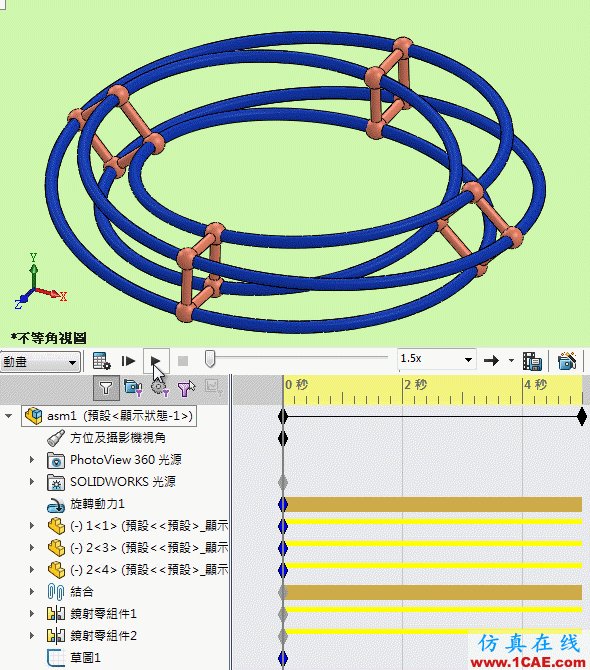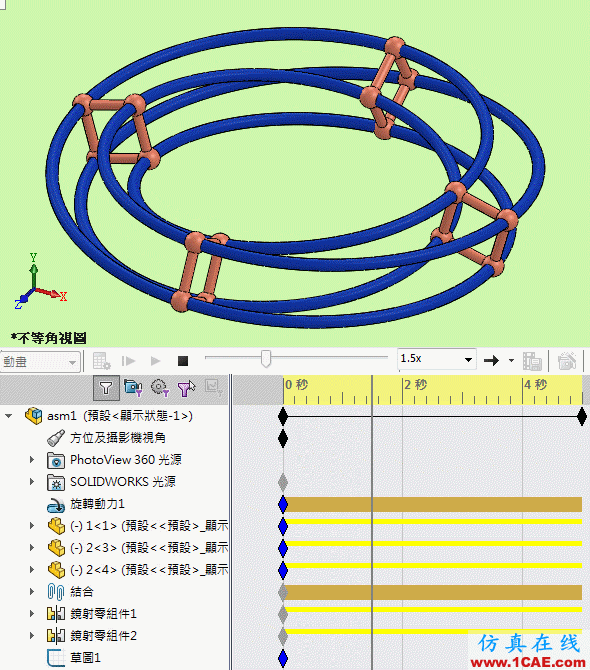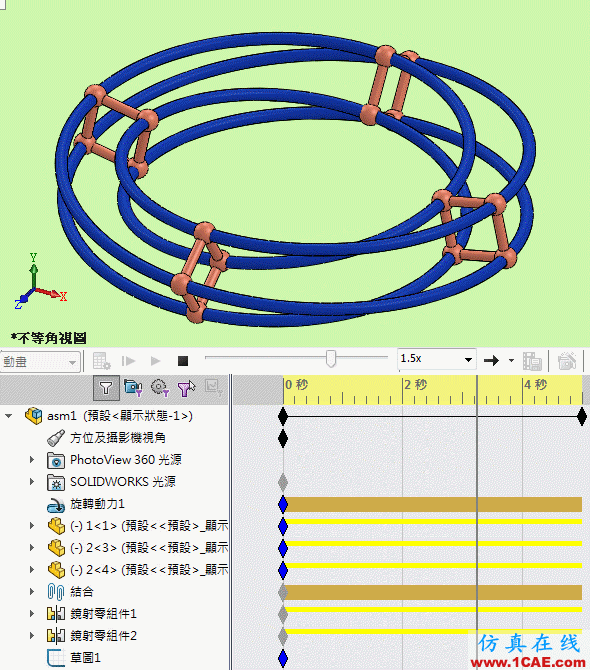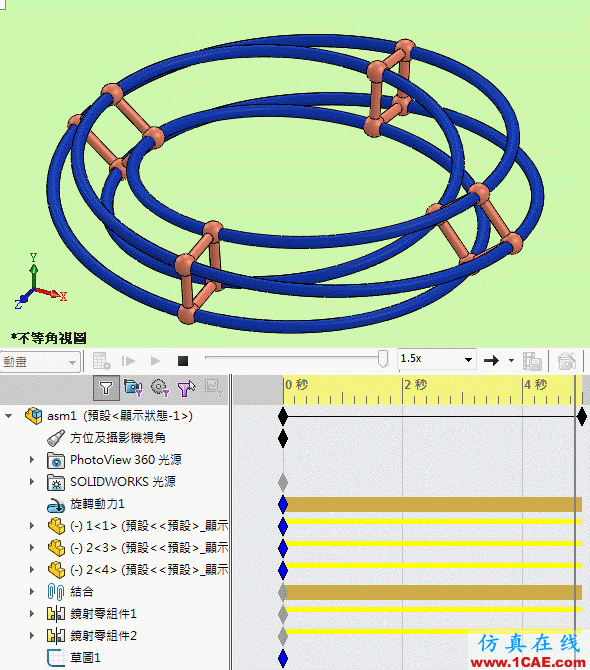
作图參考:
1.
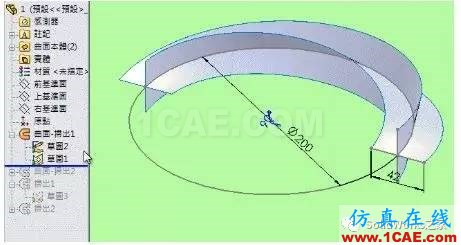
2.
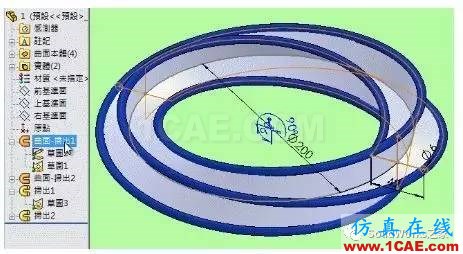
3.
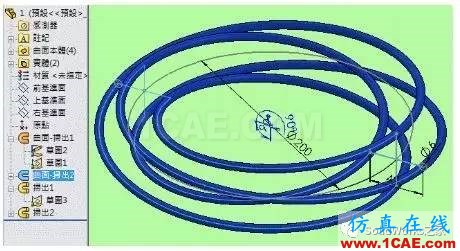
4.
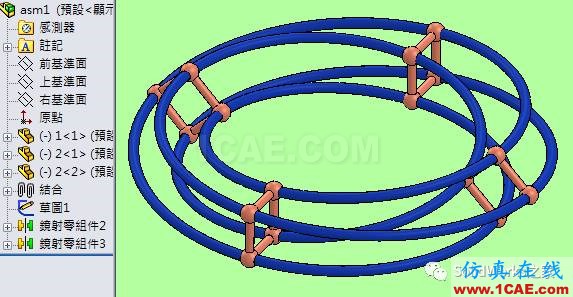
莫比乌斯简介:
莫比乌斯带常被认为是无穷大符号“∞”的创意来源,因为如果某个人站在一个巨大的莫比乌斯带的表面上沿着他能看到的“路”一直走下去,他就永远不会停下来。
公元1858年,德国数学家莫比乌斯(Mobius,1790~1868)和约翰·李斯丁发现:把一根纸条扭转180°后,两头再粘接起来做成的纸带圈,具有魔术般的性质。普通纸带具有两个面(即双侧曲面),一个正面,一个反面,两个面可以涂成不同的颜色;而这样的纸带只有一个面(即单侧曲面),一只小虫可以爬遍整个曲面而不必跨过它的边缘。这种纸带被称为“莫比乌斯带”。(也就是说,它的曲面只有一个)。
1:莫比乌斯环是一种单侧、不可定向的曲面。一张纸条扭转180°得到的莫比乌斯环是最简单的,但并不是唯一的一种。无论旋转几圈,贴上后得到的纸环,都是一种破坏了纸带原本二维结构的曲面,但都具备不可定向性和单侧性。也就是说,都具备从任意一点出发都可以回到这一点的特性。 2、3;第2点和第3点可以放在一起说,都要先看什么是手性。手性是结构及组成相同但无论怎样都不能重叠的镜像结构。而完全对称的物体是非手性的,因为稍作旋转即可重叠。所以在二维平面上的手性结构应该是非对称的几何图形,这就解释了为何你用2支笔划线却回到了原点,因为在二维的平面上,点是非手性的。你可以试用一个锐角直角三角形来重复这个实验,对于平面结构来说,非对称的图形就是手性的了,因为平面不存在翻转(即绕第3轴旋转——三维旋转)。 那么回到第2个问题,首先说结论,长铗的提法,在目前所能观测到的(即二维和三维世界里)是正确的。不过当时我看那篇文的时候,很是犹豫了一下它的理论基础是否成立。走题了,还是回到高维莫比乌斯环的问题。 个人认为,我们所看到的三维莫比乌斯环本身应该是一个2.5维的物体,因为它是一个二维纸带进行三维构象但未完全构成3维立体的产物。同理,一个3维物体如果进行高维构象,形成高维的莫比乌斯环,那么当三维手性物体在其上运行最终回到原点的时候,应处在与其原本状态成镜像的状态。 但是这时就有一个疑问,高维构象的第4维究竟是什么。扯远一点,如果真的像有些人提出的那样,时间作为第4维,那么所谓的高维莫比乌斯环就有了一个大家都非常熟悉的名字了: 轮回。 笑~顺便说一下,二维平面中的莫比乌斯环应该就是首尾相连的封闭线型,例如三角形、圆形。而二维平面中比它低维的只有一维的点,但非常遗憾,点在任何维度都不是手性的,所以难以继续验证……“莫比乌斯带”在生活和生产中已经有了一些用途。例如,用皮带传送的动力机械的皮带就可以做成“莫比乌斯带”状,这样皮带可以磨损的面积就变大了。如果把录音机的磁带做成“莫比乌斯带”状,就不存在正反两面的问题了,磁带就只有一个面了。它还能平坦的嵌入三维空间。简易的“莫比乌斯圈”可通过一张长方形纸任何一面反转粘贴。相关标签搜索:莫比乌斯转环_组件动画 SolidWorks培训课程 SolidWorks设计教程 SolidWorks视频教程 SolidWorks软件下载 SolidWorks在建筑室内设计工业设计的应用 SolidWorks基础知识 SolidWorks代做 Fluent、CFX流体分析 HFSS电磁分析 Ansys培训 Abaqus培训 Autoform培训






